Аннуитеты в МСФО
В данной статье мы продолжим говорить о дисконтировании денежных потоков и в этот раз речь пойдет об аннуитетных денежных потоках.
Что такое аннуитет?
Аннуитет – это серия одинаковых платежей через одинаковые промежутки времени. Это могут быть ежегодные, ежеквартальные, ежемесячные платежи. Например, фиксированная сумма зарплата, арендных выплат, платежей банку по кредиту и т.д.
Аннуитеты бывают пренумерандо и постнумерандо. Данные термины обозначают момент платежа. Термин пренумерандоозначает платежи в начале каждого периода, постнумерандо — в конце временного периода.
Формула аннуитета
Аннуитетные денежные потоки также можно дисконтировать, то есть определять их текущую стоимость. Например, это необходимо, когда нам нужно выбрать между двумя предлагаемых нам вариантами получения денег.
Дисконтирование аннуитетных платежей
ПРИМЕР 1. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
(Б) 5 раз по 10,000 долларов в конце каждого из следующих 5 лет.
Банковская ставка для получения кредита на данный срок составляет 10%.
На первый взгляд вариант (Б) в сумме лучше (5 х 10,000 = 50,000), чем 40,000 долларов. Но действительно ли это так? Ведь мы знаем, что у денег есть еще и «временная» стоимость. Чтобы сравнить эти два варианта между собой, надо привести их к одному моменту времени (к моменту «сейчас»), поскольку стоимость денег в разные моменты времени различна. В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость.
Для начала давайте вспомним, как выглядит формула дисконтирования:
PV = FV х 1/(1+R)n
где,
Future value (FV) – будущая стоимость Present value (PV) – текущая (дисконтированная/приведенная) стоимость. R – ставка процента (норма доходности, требуемая инвестором), N – число лет от даты в будущем до текущего момента
Коэффициенты дисконтирования, используемые для нашего примера 1/(1+R)n — это 0. 9091, 0.8264 и т.д. Только эти вычисления придется повторить 5 раз и сложить. Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая таблица:
9091, 0.8264 и т.д. Только эти вычисления придется повторить 5 раз и сложить. Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая таблица:
10,000 х 0,9091 = 9,091
10,000 х 0,8264 = 8,264
10,000 х 0,7513 = 7,513
10,000 х 0,6830 = 6,830
10,000 х 0,6209 = 6,209
Итого: 37,907
Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В итоге, пять платежей по 10,000 долларов в конце каждого года с учетом дисконтирования стоят 37,907 долларов, что немного меньше, чем 40,000 сегодня. Следовательно, при ставке 10%, 40,000 долларов сегодня будет выгоднее, чем предложенный аннуитет 5 лет по 10,000 долларов.
Формулу дисконтированной стоимости аннуитета можно записать следующим образом:
PV = PMT х [1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4 +1/(1+R)5] = 10,000 х (0.9091+0.8264+0.7513+0.6830+0. 6209) = 10,000 х 3.7907 = 37,907
6209) = 10,000 х 3.7907 = 37,907
где PMT (от английского payment) – это сумма аннуитетного платежа.
Как Вы могли заметить, вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз. Результат сложения коэффициентов дисконтирования за 5 лет называется коэффициентом аннуитета. В данном примере коэффициент аннуитета равен 3,7907.
Таким образом, для нахождения текущей стоимости аннуитетов необходимо разовый платеж умножить на коэффициент аннуитета (10,000*3,7907 = 37,907).
Итак, мы разобрали пример с аннуитетными платежами в конце каждого года (постнумерандо) .
ПРИМЕР 2. Давайте немного изменим условия нашего примера. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
Б) 5 раз по 10,000 долларов в начале каждого из следующих 5 лет.
Это будет так называемый аннуитет пренумерандо.
В данной ситуации, так как первый платеж производится в начале года, то самый важный нюанс, о котором надо помнить, это то что, первый платеж не надо дисконтировать (т. е. приводить к настоящему моменту). Другими словами, для первого платежа используется коэффициент дисконтирования равный единице. Но необходимо дисконтировать остальные 4 платежа, так как они отложены во времени. Для иллюстрации составим следующую таблицу:
е. приводить к настоящему моменту). Другими словами, для первого платежа используется коэффициент дисконтирования равный единице. Но необходимо дисконтировать остальные 4 платежа, так как они отложены во времени. Для иллюстрации составим следующую таблицу:
10,000 х 1.000 = 10,000
10,000 х 0.9091 = 9,091
10,000 х 0.8264 = 8,264
10,000 х 0.7513 = 7,513
10,000 х 0.6830 = 6,830
Итого: 41,698
Следовательно, предложенный аннуитет 5 лет по 10,000 в начале года будет выгоднее, чем 40,000 сегодня при ставке 10%.
Формула дисконтированной стоимости аннуитета:
PV = PMT + PMT х [1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4] = 10,000 + 10,000 х (0.9091+0.8264+0.7513+0.6830) = 10,000 + 10,000 х 3.1698 = 41,698
Обратите внимание, что в данном примере мы определили коэффициент аннуитета для четырех отложенных во времени платежей, а не для пяти, а первый платеж не дисконтировали.
Как видно из данных примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода.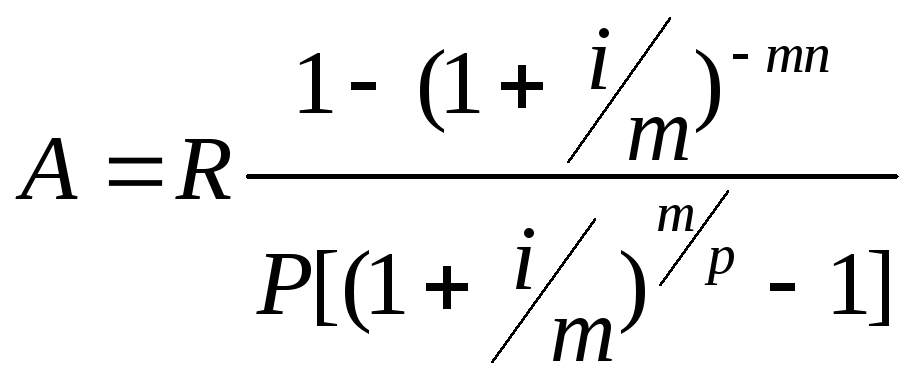 Поэтому, если нужно рассчитать дисконтированную стоимость аннуитетных денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.
Поэтому, если нужно рассчитать дисконтированную стоимость аннуитетных денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.
Все блоги
Аннуитеты. Понятие и разновидности
Денежный поток с равными интервалами и равными поступлениями денежных средств называется финансовой рентой, или аннуитетом. Различают срочные и бессрочные аннуитеты. По моменту поступления денежных средств в выбранном интервале времени срочные и бессрочные аннуитеты могут быть как потоками пренумерандо, так и потоками постнумерандо. При этом каждый из срочных аннуитетов может рассчитываться как по схеме наращения, так и по схеме дисконтирования.
Классификацию аннуитетов наглядно иллюстрирует рисунок.
Под срочным аннуитетом понимается денежный поток с поступлениями в течение ограниченного времени (срочный денежный поток) с равными по величине поступлениями денежных средств через равные промежутки времени. По моменту поступления денежных средств различают срочные аннуитеты пренумерандо и постнумерандо.
По моменту поступления денежных средств различают срочные аннуитеты пренумерандо и постнумерандо.
Срочный аннуитет постнумерандо можно рассчитать как по схеме наращения, так и по схеме дисконтирования.
Формула оценки срочного аннуитета постнумерандо по схеме наращения имеет следующий вид:
FVpst = PV (1 + r)n-1 + PV (1 + r)n—2 + … + PV (1 + r) + PV
Срочный аннуитет пренумерандо можно рассчитать как по схеме наращения, так и по схеме дисконтирования.
Формула оценки срочного аннуитета пренумерандо по схеме наращения имеет следующий вид:
FVpre=FVpst(l+ r) = PV [(1 +r)n— 1] (1 + r)/r.
Формула оценки срочного аннуитета пренумерандо по схеме дисконтирования имеет следующий вид:
PVpre = PVpst(l + r) = FV [1 — (1+r)-n ] (1 + r) / r.
Под бессрочным аннуитетом (вечная рента) понимается денежный поток с равными по величине поступлениями денежных средств в течение длительного срока через равные интервалы времени.
В случае бессрочного аннуитета поток равных платежей через равные интервалы в течение длительного периода времени рассматривается как бесконечный. При этом подразумевается, что в рамках выбранного интервала осуществляется только один платеж. В этой связи бессрочный аннуитет математически можно представить как бесконечность (n -> ∞) или как бесконечно убывающую геометрическую прогрессию.
Бессрочный аннуитет (как разновидность денежного потока) можно классифицировать по моменту поступлений в выбранном интервале времени на потоки пренумерандо и постнумерандо. Однако, в отличие от других денежных потоков, которые можно рассчитывать как по схеме наращения, так и дисконтирования, оценка бессрочного аннуитета способом наращения не имеет смысла, так как поток стремится к бесконечности и нельзя определить п. Поэтому единственным способом остается обратный способ (способ дисконтирования).
При этом сначала рассчитывается приведенная стоимость бессрочного аннуитета постнумерандо, а затем с его помощью приведенная стоимость бессрочного аннуитета пренумерандо. Классификация способов оценки бессрочных аннуитетов приведена в таблице.
Способы оценки бессрочных аннуитетов
|
По моменту поступления денежных средств в выбранном временном интервале |
Оценка бессрочного аннуитета |
|
|
по схеме наращения |
по схеме дисконтирования |
|
|
1) потоки с поступлениями в начале выбранного интервала времени — пренумерандо; |
Не имеет решения |
Бессрочный аннуитет пренумерандо |
|
2) потоки с поступлениями в конце выбранного интервала времени — постнумерандо. |
Не имеет решения |
Бессрочный аннуитет постнумерандо |
Формула оценки бессрочного аннуитета постнумерандо по схеме дисконтирования имеет следующий вид:
PVpst=A/r,
где А — одно денежное поступление за выбранный временной интервал.
Данная формула показывает, что приведенную стоимость можно рассчитать даже для денежного потока с неограниченным количеством платежей. Так, при сроке аннуитета, превышающем 50 лет, и процентной ставке, равной 10%, разница между значениями коэффициентов дисконтирования незначительная. Чем выше значение процентной ставки, тем меньше срок, при превышении которого разница между значениями коэффициента дисконтирования становится несущественной.
Формула оценки бессрочного аннуитета пренумерандо по схеме дисконтирования имеет следующий вид:
PVpre = PVprs+ A
где PVpre — поток пренумерандо;
PVpre — поток постнумерандо;
А — величина первого платежа.
Как следует из данной формулы, приведенная стоимость бессрочного аннуитета пренумерандо превышает приведенную стоимость бессрочного аннуитета постнумерандо на величину первого платежа.
CFA — Как рассчитывать приведенную стоимость (PV) серии денежных потоков (аннуитета и перпетуитета)? | программа CFA
См. начало:
Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.
Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.
Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.
Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.
Расчет текущей стоимости (PV) серии равных денежных потоков.
 N} \over r \right]} \) (формула 11)
N} \over r \right]} \) (формула 11)Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим текущую стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в формуле 11.
Пример расчета текущей (приведенной) стоимости обычного аннуитета.
Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1 000 каждый год в течение 5 лет с первым платежом через год.
Норма прибыли составляет 12% в год.
Сколько вы должны заплатить за этот актив?
Решение:
Чтобы узнать стоимость финансового актива, используйте формулу (11) текущей стоимости обычного аннуитета, со следующими данными:
A = €1,000
r = 12% = 0.12
N = 5
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \left[ 1-{1\over(1. 5} \over 0.12 \right] \end{aligned} } \)
5} \over 0.12 \right] \end{aligned} } \)
= €1,000 * (3.604776)
= €3,604.78
Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.
Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).
При авансовом аннуитете 1-ый платеж выполняется в текущую дату (t = 0). В общей сложности авансовый аннуитет включает N платежей.
На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.
Авансовый аннуитет в размере $100 за период.
На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:
- единовременная сумма в размере $100 на текущую дату (при t = 0) и
- обычный аннуитет в размере $100 за период в течение 3-х периодов.
 {-N} \over r \right] (1+r) } \)
{-N} \over r \right] (1+r) } \)Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.
Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.
Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.
Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:
- немедленную единовременную выплату в размере $2 млн. или
- аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.
Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.
Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.
 {19}} \over 0.07 \right] \end{aligned} } \)
{19}} \over 0.07 \right] \end{aligned} } \)
= $200,000(0.335595)
= $2,067,119.0519 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.
Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.
Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.
Пример расчета прогнозируемой текущей стоимости обычного аннуитета.
Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при t = 10.
После того, как пособия начнут выплачиваться, эти выплаты продлятся до t = 39, что составляет в общей сложности 30 платежей.
Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионному плану составляет 5% годовых, начисляемых ежегодно?
Решение:
Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при t = 10.
 {30}} \over 0.05 \right] \end{aligned} } \)
{30}} \over 0.05 \right] \end{aligned} } \)
= €1,000,000 * (15.372451)
= €15,372,451.03Текущая стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).
На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от t = 10 до t = 39.
Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени t = 9.
Текущая стоимость (PV) пенсионных пособий по состоянию на t = 9 составляет €15,372,451.03.
Далее задача заключается в том, чтобы найти текущую стоимость на текущую дату (при t = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости (см. CFA — Эквивалентность приведенной и будущей стоимости денежных потоков).
Как показано на временной лини, мы можем рассматривать сумму при t = 9 в качестве будущей стоимости с точки зрения t = 0.
Мы вычислим текущую стоимость (PV) при t = 0 следующим образом:
FVN = €15,372,451.
 t \right] } \) (формула 12)
t \right] } \) (формула 12)Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:
PV = A / r (формула 13)
Чтобы понять смысл этого преобразования, обратите внимание на формулу (11) текущей стоимости обычного аннуитета.
Поскольку N (количество периодов в аннуитете) переходит на бесконечность, выражение 1 / (1 + r)N приближается к 0, а формула 11 упрощается до формулы 13.
Эта формула потребуется, когда мы будем оценивать дивиденды от акций, поскольку акции не имеют предопределенного срока действия.
Акция, выплачивающая постоянные дивиденды, аналогична бессрочному аннуитету.
При первом платеже через год от текущей даты, перпетуитет в размере $10 в год при 20%-ой норме прибыли имеет текущую стоимость в размере $10 / 0,2 = $50 долларов.
Формула 13 справедлива только для бессрочного аннуитета с равными платежами.
 В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.
В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.
Пример расчета текущей стоимости (PV) перпетуитета.
Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’), которые обеспечивают равные денежные выплаты в течение неограниченного срока.
Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?
Решение:
Чтобы ответить на этот вопрос, мы можем использовать формулу 13 со следующими данными:
A = £100
r = 5% = 0. 05
05PV = A/r
= £100/0.05
= £2,000Облигация будет стоить £2 000.
Текущая стоимость на момент времени, отличный от текущей даты (t = 0).
На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от t = 0.
Если мы рассчитаем перпетуитет, начинающийся с платежа в размере $100 на 2-й год, то мы получим PV1 = $ 100 / 0,05 = $2 000 при 5%-й ставке. Кроме того, мы можем рассчитать PV на текущую дату как PV0 = $2,000 / 1.05 = $ 1,904.76.
Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.
По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.

При процентной ставке 5% денежные потоки в размере $6 в год, начинающиеся в конце 4-го года, будут стоить $34,72 на конец 3-го года (t = 3) и $29,99 на текущую дату (t = 0).
Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.
Пример расчета текущей стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.
Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при t = 5.
Какова будет его текущая стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?
Решение:
Во-первых, мы находим текущую стоимость перпетуитета при t = 4, а затем дисконтируем эту сумму к текущей дате t = 0. (Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс t = 4 для нашего расчета текущей стоимости).

1. Находим текущую стоимость перпетуитета при t = 4:
A = £100
r = 5% = 0.05PV = A/r
= £100/0.05
= £2,0002. Находим текущую стоимость будущего значения при
t = 4.С точки зрения сегодняшней даты t = 0 текущую стоимость в £2,000 можно считать будущей стоимостью.
Теперь нам нужно найти текущую стоимость £2,000 при
t = 0:FVN = £2,000 (текущая стоимость при t = 4)
r = 5% = 0.05
N = 4PV = FVN * (1 + r)—N
= £2,000 * (1.05)-4
= £2,000 * (0.822702)
= £1,645.40Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.
Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.

В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при t = 5; после этого платежи продолжаются бесконечно.
Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к t = 5.
Благодаря этому перпетуитет с отсроченной 1-й выплатой (до t = 5) обеспечивает выплаты при t = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.
Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.
Следующий пример иллюстрирует этот результат.
Пример расчета текущей стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.
С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:
- Перпетуитет 1 на £100 в год, начиная с 1-го года (первый платеж при t = 1).

- Перпетуитет 2 на £100 в год, начиная с 5-го года (первый платеж при t = 5).
Решение:
Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при t = 1, 2, 3, 4).
Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:
PV0 (Перпетуитет 1) = £100 / 0.05 = £2,000
PV4 (Перпетуитет 2) = £100 / 0.05 = £2,000
PV0 (Перпетуитет 2) = £2,000 / (1.05)4 = £1,645.40PV0 (Аннуитет)
= PV0 (Перпетуитет 1) — PV0 (Перпетуитет 2)
= £2,000 — £1,645.40
= £354.60Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.
Как вычислять текущую стоимость (PV) для серии неравных денежных потоков?
Когда мы имеем неравные денежные потоки, мы должны сначала найти текущую стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.

Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.
В таблице ниже приведена последовательность денежных потоков с
- временными периодами в 1-м столбце,
- денежными потоками во 2-м столбце и
- текущей стоимостью (PV) каждого денежного потока в 3-м столбце.
В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.
Серия неравных денежных потоков и их приведенная стоимость при ставке 5%. Период
Денежный поток ($)
PV при t=0
1
1,000
$1,000(1.05)-1 =
$952.
 38
382
2,000
$2,000(1.05)-2 =
$1,814.06
3
4,000
$4,000(1.05)-3 =
$3,455.35
4
5,000
$5,000(1.05)-4 =
$4,113.51
5
6,000
$6,000(1.05)-5 =
$4,701.16
Сумма =
$15,036.
 46
46Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.
Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.
Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду t = 5:
PV = $15,036.46
N = 5
r = 5% = 0.05FVN = PV * (1 + r)N
= $15,036.46 * (1.05)5
= $15,036.46 * (1.276282)
= $19,190.76См. далее:
CFA — Как рассчитывать будущую стоимость (FV) последовательности денежных потоков (аннуитета)? | программа CFA
См.
 начало:
начало:При оценке денежных потоков, последовательно осуществляемых в течение многих периодов времени, обычно используются следующие термины:
- Аннуитет (англ. ‘annuity’) — это ограниченная последовательность (серия) денежных потоков.
- Обычный или простой аннуитет или аннуитет постнумерандо (англ. ‘ordinary annuity’) — это серия денежных потоков, в которой денежные потоки происходят через 1 период, т.е. в начале следующего периода или в конце текущего периода (например, 1-й поток индексируется как t = 1).
- Авансовый аннуитет или аннуитет пренумерандо (англ. ‘annuity due’) — это серия денежных потоков, в которой денежные потоки происходят немедленно, т.е. в начале текущего периода (1-й поток индексируется как t = 0).
См. примеры расчета авансового аннуитета. - Бессрочный аннуитет или перпетуитет или вечная рента (англ.
 ‘perpetuity’ или ‘perpetual annuity’) — это бесконечная (бессрочная) серия потоков денежных средств. При этом первый денежный поток происходит через один период (т.е. t = 1).
‘perpetuity’ или ‘perpetual annuity’) — это бесконечная (бессрочная) серия потоков денежных средств. При этом первый денежный поток происходит через один период (т.е. t = 1).
См. пример расчета перпетуитета.
Как вычислять обычный аннуитет, то есть FV равных денежных потоков?
Рассмотрим обычный аннуитет с начислением 5% годовых.
Предположим, что у нас есть 5 отдельных депозитов по $1 000, поступающих с равными интервалами, каждый из которых составляет 1 год, причем 1-й платеж происходит при t = 1.
Наша цель — найти будущую стоимость (FV) этого обычного аннуитета после внесения последнего депозита при t = 5. Поскольку все 5 депозитов вносятся с периодичностью в 1 год, последний платеж осуществляется через 5 лет.
Будущая стоимость (FV) пятилетнего обычного аннуитета.
Как показывает временная линия на рисунке выше, мы находим будущую стоимость каждого депозита на сумму $1 000 к моменту времени t = 5, используя для каждого депозита формулу FV (2):
FVN = PV * (1 + r)N.

Стрелки на рисунке выше соответствуют дате каждого депозита от даты 1-го платежа до t = 5 и указывают на расчет будущей стоимости FV для соответствующего депозита.
Например, по 1-му депозиту в размере $1 000 (при t = 1) будут начисляться проценты в течение 4-х последующих периодов.
Используя формулу FV, мы вычисляем будущую стоимость 1-го депозита при t = 5, которая составляет:
$1 000 * (1,05)4 = $1 215,51.
Для всех других платежей мы вычисляем FV аналогичным образом.
Обратите внимание, что мы находим будущую стоимость при t = 5, поэтому последний (5-й) платеж не важен и не отображается на временной линии.
Теперь, имея все значения FV при t = 5, мы можем их суммировать, чтобы получить будущую стоимость аннуитета, т.е. всей последовательности равных денежных потоков. Эта сумма составляет $5 525,63.
Теперь рассмотрим общую формулу аннуитета, в которой:
- A — сумма аннуитета,
- N — количество периодов и
- r — процентная ставка за период.
 N — 1} \over r \right] }$$
N — 1} \over r \right] }$$FVN = A * [((1 + r)N -1) / r] (формула 7)
Выражение в квадратных скобках — это фактор будущей стоимости аннуитета (англ. ‘future value annuity factor’).
Этот коэффициент означает будущую стоимость обычного аннуитета на одну денежную единицу (т.е. на $1 в нашем примере).
Умножение фактора будущей стоимости аннуитета на сумму аннуитета дает будущую стоимость обычного аннуитета.
Для обычного аннуитета, изображенного на рисунке выше, фактор будущей стоимости аннуитета из формулы 7 можно рассчитать как:
[((1.05)5 — 1) / 0.05] = 5.525631.
Если сумма аннуитета A = $1 000, то будущая стоимость аннуитета составляет $1,000 * (5.525631) = $5,525.63, что соответствует вычислению, сделанному ранее.
Следующий пример иллюстрирует, как можно рассчитать будущую стоимость обычного аннуитета, используя формулу 7.

Пример расчета будущей стоимости простого аннуитета.
Предположим, что пенсионный план вашей компании с установленными взносами позволяет вам инвестировать до €20 000 в год. Вы планируете инвестировать €20 000 в год в индексный инвестиционный фонд в течение следующих 30 лет.
Исторически сложилось так, что этот фонд в среднем приносил своим инвесторам 9% в год.
Исходя из того, что вы будете зарабатывать 9% в год, сколько пенсионных средств будет на вашем счете после внесения последнего платежа?
Решение:
Используйте формулу 7, чтобы найти будущую стоимость аннуитета:
A = €20,000
r = 9% = 0.09
N = 30Фактор FV аннуитета = [(1 + r)N — 1] / r
= [(1.09)30 — 1] / 0.09 = 136.307539.FVN = €20,000 * (136.307539) = €2,726,150.77.
Предполагая, что фонд будет зарабатывать в среднем 9% в год, вы получите €2,726,150.
 77 к моменту выхода на пенсию.
77 к моменту выхода на пенсию.Как вычислять аннуитет при неравных денежных потоках?
Довольно часто последовательность денежных потоков аннуитета неравномерна. То есть, потоки денежных средств не являются одинаковыми платежами, осуществляемыми через равные периоды времени.
Это исключает использование в расчете фактора будущей стоимости аннуитета.
Например, у инвестора может быть план сбережений, который предполагает неравные денежные выплаты в зависимости от месяца года или более низкие сбережения во время запланированного отпуска.
В этом случае будущую стоимость серии неравных денежных потоков можно вычислить, рассчитав и суммировав FV каждого отдельного денежного потока.
Пример расчета аннуитета при неравномерных денежных потоках.
Предположим, что у вас есть 5 денежных потоков, которые описаны в таблице ниже. Платежи пронумерованы относительно текущей даты (t = 0).
Серия неравных денежных потоков и их будущая стоимость при ставке 5%. 
Год
Денежный
поток, $Будущая стоимость
на 5-й годt = 1
1,000
$1,000 (1.05)4 =
$1,215.51
t = 2
2,000
$2,000(1.05)3 =
$2,315.25
t = 3
4,000
$4,000(1.05)2 =
$4,410.00
t = 4
5,000
$5,000(1.
 05)1 =
05)1 =$5,250.00
t = 5
6,000
$6,000(1.05)° =
$6,000.00
Сумма =
$19,190.76
Все платежи, указанные в таблице выше, отличаются по сумме. Поэтому самый прямой подход к расчету будущей стоимости этих инвестиций при t = 5, — это вычисление FV каждого отдельного платежа при t = 5, а затем суммирование найденных значений FV.
Совокупная FV на 5-й год равна $19,190.76, как показано в третьем столбце таблицы.
См. далее:
4 Финансовые потоки и их анализ
Тема 4
Финансовые потоки и их анализ
Одной из базовых концепций теории финансов является концепция денежных потоков.

Денежные потоки – это кровеносная система деятельности любого предприятия любой формы собственности.
В результате реализации какого-либо проекта или функционирования того или иного вида активов образуется денежный поток с элементами которые генерируются через временные интервалы
При рассмотрении денежных потоков мы будем исходить из следующих допущений:
1) элементы денежного потока могут быть либо независимыми, либо связанными между собой определенным алгоритмом;
Рекомендуемые файлы
2) элементы денежного потока будем считать однонаправленными;
3) элементы денежного потока могут иметь место либо в начале, либо конце временного периода т.е. не рассредоточены внутри периода, а сконцентрированы на одной из его границ;
Если элементы денежного потока сконцентрированы в его начале, то такой поток называется потоком пренумерандо. Если элементы денежного потока имеют место в конце временного периода, то такой денежный поток называется потоком постнумерандо.

4) временные периоды между отдельными элементами денежного потока чаще всего принимаются равными.
На практике большее распространение получил поток постнумерандо, в частности, именно этот поток лежит в основе методик анализа инвестиционных проектов. Некоторые объяснения этому можно дать исходя из общих принципов учета, согласно которым принято подводить итоги и оценивать финансовый результат того или иного действия по окончании очередного отчетного года.
Что касается поступления денежных средств в счет оплаты, то на практике они, естественно, распределены во времени неравномерно и поэтому удобнее условно отнести их к концу временного периода.
Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.
Оценка денежного потока может выполняться в рамках решения двух задач:
1) т. н. прямая задача – предполагает суммарную оценку наращенного денежного потока, т.е. в ее основе лежит будущая стоимость;
2) т.
 н. обратная задача предполагает суммарную оценку дисконтированного (приведенного) денежного потока.
н. обратная задача предполагает суммарную оценку дисконтированного (приведенного) денежного потока.При рассмотрении денежных потоков ключевым моментом является предпосылка по умолчанию о том, что анализ денежных потоков проводится с позиции т.н. «разумного инвестора».
Именно этим и объясняется тот факт, что при оценке будущих потоков как при реализации процессов наращения, так и при реализации процессов дисконтирования предполагается только капитализация ранее начисленных, но не востребованных процентов.
Аннуитет.
Одним из ключевых понятий в финансовых расчетах является понятие аннуитета.
Аннуитет – это частный случай денежного потока, а именно – это такой денежный поток, у которого длительность всех периодов равны между собой. Аннуитет в финансовой литературе часто называют финансовой рентой или просто рентой.
Любое денежное поступление называется членом ренты, а величина постоянного временного интервала между двумя последовательными денежными поступлениями называется периодом аннуитета (ренты).

Если число равных временных интервалов ограничено, аннуитет называется срочным.
Если в течение каждого базового периода начисления процентов на денежные поступления происходит р раз, то аннуитет называют р-срочным.
Как и в общем случае оценки денежных потоков применительно к аннуитетам выделяют два типа аннуитетов: пренумерандо и постнумерандо.
Примером срочного аннуитета постнумерандо могут служить регулярно поступающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истечении очередного периода.
В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления достаточной суммы для крупной покупки.
Переменный аннуитет постнумерандо.
Ситуация, когда денежные поступления по периодам варьируют, является наиболее распространенной.
 В этом случае аннуитет называется переменным.
В этом случае аннуитет называется переменным.В этом случае общая постановка задачи такова.
Пусть — аннуитет, период которого совпадает с базовым периодом начисления процентов по ставке . Требуется оценить стоимость данного аннуитета с позиции будущего и с позиции настоящего (т.е. решить прямую и обратную задачу оценки денежного потока).
Прямая задача предполагает оценку денежного потока с позиции будущего, т.е. когда реализуется схема наращения. Для переменного аннуитета постнумерандо эта схема имеет следующий вид (см. рис.).
Следовательно, наращенный денежный поток для исходного потока постнумерандо имеет вид:
Формула для определения будущей стоимости переменного аннуитета постнумерандо:
.
Если для определения будущей стоимости переменного аннуитета постнумерандо использовать финансовые таблицы, то формула принимает следующий вид:
.
Обратная задача подразумевает оценку денежного потока с позиции текущего момента, т.е. на момент начала первого периода. В этом случае реализуется задача дисконтирования и суммирование проводится по дисконтированному денежному потоку. В этом случае приведенный денежный поток исходного потока постнумерандо имеет вид:
.
Приведенная стоимость переменного аннуитета постнумерандо определяется по формуле:
Если пользоваться финансовыми таблицами, то вышеприведенная формула примет вид:
.
Пример.
Рассчитать приведенную стоимость переменного аннуитета постнумерандо (тыс. грн.): 12, 15, 9, 25, если заданная процентная ставка составляет 12% и период равен одному году.
Год
Денежный поток, тыс. грн.
Дисконтный множитель при r= 12%
Приведенный поток, тыс. грн.
1
12
0,8929
10,71
2
15
0,7972
11,96
3
9
0,7118
6,41
4
25
0,6355
15,89
61 44,97
Переменный аннуитет пренумерандо.
Логика оценки переменного аннуитета пренумерандо аналогична ранее рассмотренной задачи. Некоторое расхождение в расчетных формулах объясняется тем, что элементы денежного потока сдвигаются к началу соответствующего временного интервала.
Для прямой задачи наращенный денежный поток имеет вид:
.
Будущая стоимость исходного переменного аннуитета пренумерандо может быть рассчитана по следующей формуле:
.
Между денежными потоками пренумерандо и постнумерандо имеет место следующая зависимость:
.
Для обратной задачи оценки переменного аннуитета постнумерандо приведенный денежный поток имеет вид:
Приведенная стоимость переменного аннуитета пренумерандо может быть рассчитана по формуле:
.
Как и в случае с будущей стоимостью .
Постоянный аннуитет постнумерандо.
Аннуитет называется постоянным, если все денежные поступления равны между собой. В этом случае .
Для оценки будущей и приведенной стоимости аннуитета можно пользоваться ранее рассмотренными вычислительными формулами. Однако, благодаря специфике постоянных аннуитетов в отношении равенства денежных поступлений эти формулы могут быть существенно упрощены.
Прямая задача оценки срочного постоянного аннуитета постнумерандо при заданных величинах регулярного денежного поступления А и процентной ставке r предполагает оценку будущей стоимости аннуитета .
Как следует из логики, присущей схеме постоянного аннуитета постнумерандо, записанный в порядке поступления платеже наращенный денежный поток имеет вид:
.
Откуда формулы для определения будущей стоимости принимают следующий вид:
или
Входящий в формулу множитель называется коэффициентом наращения ренты (аннуитета) и представляет собой сумму первых членов геометрической прогрессии с знаменателем 1+r.
Таким образом, .
Откуда .
Экономический смысл множителя заключается в следующем: он показывает, чему будет равна суммарная величина срочного постоянного аннуитета в одну денежную единицу к концу срока его действия.
При этом предполагается, что производится только начисление денежных сумм, а их изъятие может быть сделано только по окончании срока действия аннуитета.
Величина факторного множителя зависит от величины процентной ставки м срока действия аннуитета, причем с увеличением каждого из этих параметров величина множителя возрастает.
Значения факторного множителя для различных сочетаний процентной ставки и длительности периода табулированы и представлены в финансовых таблицах.
Факторный множитель показывает, во сколько раз наращенная сумма аннуитета больше величины денежного поступления А.
В этой связи его называют также коэффициентом аккумуляции вкладов.
Пример.
Вам предлагается сдать в аренду участок на три года, выбрав один из двух вариантов оплаты аренды: а) по 10 тыс. грн. в конце каждого года; б) 35 тыс. грн. в конце трехлетнего периода.
Какой вариант предпочтительнее, если банк предлагает 20% годовых по вкладам?
тыс. грн.
Таким образом, расчет показывает, что вариант а) выгоднее.
Нами рассмотрен наиболее общий вариант постановки задачи, когда денежные поступления имеют место один раз в конце периода и сложные проценты начисляются один раз за период.
Так как логика срочных постоянных аннуитетов довольно часто встречается в финансовых контрактах, есть необходимость рассмотреть и другие возможные варианты финансовых условий, а именно: денежные поступления могут иметь место несколько раз за период, начисление процентов может проводиться не только ежегодно, но и несколько раз на год, может использоваться не только схема сложных, но и схема простых процентов и пр.
Постоянный аннуитет постнумерандо с начислением процентов m – раз за период.
Если r является процентной ставкой за базовый период, а начисление сложных процентов происходит m раз в течение этого периода, то наращенный денежный поток, начиная с последнего денежного поступления, имеет вид:
.
Другими словами, мы получили геометрическую прогрессию, первый член которой равен А и знаменатель которой — . Следовательно, сумма первых n членов этой прогрессии будет равна:
Другой очень важной ситуацией, которая часто встречается в финансовых операциях, является ситуация, когда в течение базового периода начисления процентов денежные поступления происходят несколько раз, а проценты начисляются один раз в конце периода.
В рамках этой ситуации возможно решение двух задач:
1) используется для начисления схема сложных процентов;
2) используется схема простых процентов.
Рассмотрим первую из них.
Пусть в течение базового периода денежные поступления происходят p раз и один раз в конце периода начисляются сложные проценты в соответствии с ставкой r.
На последнее поступление проценты не начисляются и оно остается равным А. На предпоследнее р – 1 поступление начисляются сложные проценты за часть периода 1/р и оно будет равно . На р – 2 поступление начисляются сложные проценты на часть периода 2/р и оно будет равно и т.д. до первого денежного поступления включительно, которое будет равно . Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом А, знаменателем и числом членов, равным р.
Поэтому будущая стоимость такого аннуитета будет определяться из выражения:
, или .
Поскольку , значения в финансовых таблицах как правило не приводятся. Поэтому для расчета коэффициента наращения такого аннуитета пользуются формулой: .
Рассмотрим вторую задачу, полагающую, что на отдельные взносы, поступающие в течение периода, происходит начисление простых процентов. Для этого определим сумму, которая накопится к концу любого периода.
Как и в предыдущем случае на последнее р-е поступление денежных средств проценты не начисляются и оно остается равным А.
На предпоследнее поступление за период р – 1 начисляются простые проценты за 1/р — часть периода и оно будет равно
Аналогичным образом предшествующее (р –2) – е поступление станет равным и т.д. Наконец, первое поступление будет равняться .
Полученные величины образуют арифметическую прогрессию (разность равна; число членов р), следовательно сумма членов такой прогрессии будет равна:
Таким образом, имеем дело с аннуитетом, в котором денежные поступления в каждом периоде равны величине .
Для определения будущей стоимости такого аннуитета используется формула: .
Рассмотрим самую общую ситуацию, когда в течение базового периода денежные поступления происходят р раз и проценты начисляются m за период. Здесь возможны две ситуации: либо начисляются простые проценты, либо — сложные.
Если происходит начисление только сложных процентов, то, как и ранее, определяем вначале сумму, образовавшуюся в конце любого периода.
Последнее поступление в периоде остается равным А, т.к. на него не производится начисление процентов. Предпоследнее поступление после начисления сложных процентов составит Предшествующее ему поступление — и т. д. вплоть до первого, которое станет равным Сумма полученных величин составит:
Будущая стоимость аннуитета с денежными поступлениями, равными полученной сумме, определяется по формуле:
Пример.
Вам предлагается сдать в аренду участок с арендной платой в размере 5 тыс. грн. в конце каждого полугодия. При этом возможно начисление процентов: а) ежегодное; б) полугодовое; в) ежеквартальное.
Какой из вариантов предпочтительнее?
а) ежегодное начисление процентов.
Возможно либо начисление сложных, либо простых процентов.
Будущая стоимость аннуитета при начислении сложных процентов:
тыс. грн.
Если в течение года начисляются простые процента, то будущая стоимость аннуитета составит:
тыс. грн.
б) начисление процентов по полугодиям:
тыс. грн.
в) ежеквартальное начисление процентов:
тыс. грн.
Обратная задача оценки постоянного срочного
аннуитета постнумерандо.
В этом случае производится оценка будущих денежных поступлений с позиции текущего момента, под которым понимается момент времени, начиная с которого отсчитываются равные временные интервалы, входящие в аннуитет.
Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо выводится из ранее выведенной основной формулы и имеет вид:
Множитель называется коэффициентом дисконтирования ренты и как сумма членов геометрической прогрессии равен величине:
.
Экономический смысл дисконтного множителя заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярным денежным поступлением в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r. Значения этого множителя табулированы в финансовых таблицах.
Дисконтный множитель можно интерпретировать и как величину капитала, поместив который в банк под сложную процентную ставку r, можно обеспечить регулярные выплаты в размере одной денежной единицы в течение n периодов.
Из ранее выведенной формулы для определения множителя следует, что при возрастании процентной ставки величина множителя уменьшается и, таким образом, уменьшается величина приведенной стоимости.
В случае рассмотрения только сложных процентов формулы для нахождения приведенных стоимостей аннуитетов аналогичны формулам для нахождения наращенных сумм. Получающиеся при этом денежные потоки будут представлять собой геометрические прогрессии, знаменателями которых будут соответствующие дисконтные множители.
Так, для постоянного аннуитета постнумерандо с начислением сложных процентов m раз за базовый период приведенный денежный поток имеет вид:
Следовательно, приведенная стоимость такого аннуитета будет равна:
Для р-срочных аннуитетов с начислением сложных процентов соответственно один раз за базовый период и m раз за базовый период аналогичным образом можем получить следующие формулы для определения приведенной стоимости:
Пример.
Страховая компания, заключив на 4 года договор с некоторой фирмой, получает от нее страховые взносы по 20 тыс. грн. в конце каждого полугодия. Эти взносы компания помещает в банк под 12% годовых.
Необходимо найти приведенную стоимость суммы, которую получит страховая компания по данному контракту, если проценты будут начисляться: а) раз в полгода; б) ежемесячно.
а) полугодовое начисление процентов:
n = 4, r = 12%, m = 2, p = 2.
тыс. грн.
б) ежемесячное начисление процентов:
n = 4, r = 12%, m = 12, p = 2.
тыс. грн.
Отсроченный аннуитет постнумерандо.
В практике финансовых операций имеют место соглашения, когда первый из потока платежей начинает поступать не сразу, а через h периодов.
Предположим, что платежи поступают в течение периодов и сложные проценты по ставке начисляются один раз в конце базового периода, совпадающего с периодом аннуитета.
Стоимость этого аннуитета на начало периода, когда поступает первый платеж, находится по формуле и затем, осуществляя учет полученной величины за периодов, определяем приведенную стоимость отсроченного аннуитета на начальный момент времени.
Для этой цели используется следующая формула:
Из приведенной формулы видно, что приведенная стоимость отсроченного аннуитета представляет собой разность приведенных стоимостей аннуитетов с платежами, начиная с первого периода.
Пример.
Банк предлагает ренту постнумерандо на 10 лет с ежеквартальной выплатой 100 грн. Годовая процентная ставка в течение всего периода остается постоянной. По какой цене можно приобрести такую ренту, если выплаты начнут осуществляться: а) немедленно; б) через 2 года; в) через 3,5 года, а процентная ставка равна 2, 4, 12% годовых.
а) вариант немедленного начала выплат.
n = 10*4 = 40, r = 2%:4 = 0,5%.
грн.
б) вариант начала выплат через 2 года.
N = 40, r = 4% : 4 = 1%, h = 2*4 = 8.
грн.
в) вариант начала выплат через 3,5 года.
n = 40, r = 12% : 4 = 3%, h = 3,5 *4 = 14.
грн.
Из рассмотренного примера видно, что с ростом процентной ставки и срока, после которого начнутся выплаты, приведенная стоимость аннуитета уменьшается. Так, если выплаты начнутся через 3,5 года и процентная ставка составит 12% годовых, то указанную ренту можно приобретать за 1528,15 грн. или, естественно, дешевле. В то же время приведенная стоимость ренты с отсрочкой выплаты на 2 года и при процентной ставке 4% годовых составляет вдвое больше – 3032,23 грн.
Как следует из формулы для определения будущей стоимости аннуитета постнумерандо в самом общем виде
для нахождения будущей стоимости необходимо, чтобы были заданы значения следующих параметров: A, r, n, m, p. Однако, при заключении некоторого контракта уже заранее может быть задана будущая стоимость аннуитета, а необходимо определить, например, величину разовых денежных поступлений А. В этом случае при заданных значениях остальных параметров, величина разового денежного поступления может быть определена по формуле:
Если известна приведенная стоимость и остальные параметры, а необходимо найти величину разового платежа, то используется формула:
Величину разового платежа можно определить иначе. Мы помним, что Значит, , откуда с помощью несложных преобразований, получим:
Аналогичным образом можно получить формулу для определения величины разового платежа (или поступления), если имеет место аннуитет постнумерандо и задана его приведенная стоимость. В этом случае формула имеет вид:
Пример.
Работник заключает с фирмой контракт, согласно которому в случае его постоянной работы на фирме до выхода на пенсию в 65 лет фирма обязуется перечислять в конце каждого года в течение 20 лет на счет работника в банке одинаковые суммы, которые обеспечат работнику после выхода на пенсию ежегодные дополнительные выплаты в 6000 тыс. грн. в течение 15 лет.
Какую сумму каждый год должна перечислять фирма, если работнику 45 лет и предполагается, что банк гарантирует годовую процентную ставку 10% годовых?
грн.
грн.
Зачастую при заключении финансовых контрактов имеют место случаи, когда заданы все остальные параметры, а необходимо определить срок действия аннуитета. В этом случае исходим из базовой формулы будущей стоимости аннуитета:
Из этой формулы путем несложных преобразований получим:
Если решается обратная задача оценки срочного аннуитета постнумерандо и необходимо определить срок действия такого аннуитета, то в этом случае применяется формула:
Пример.
Предприятие хочет создать фонд в размере 200 тыс. грн. С этой целью в конце каждого года предприятие предполагает втосить по 50 тыс. грн. в банк под 18% годовых.
Найти срок, необходимый для создания фонда.
года
Если известны все параметры аннуитета кроме величины процентной ставки, то в этом случае используется метод линейной интерполяции, так как непосредственно из ранее приведенных формул величину процентной ставки определить нельзя.
Рассмотрим метод линейной интерполяции на конкретном примере.
Пример.
В течение 4-х лет предполагается создать резервный фонд в размере 20 тыс. грн., для чего будут производиться ежегодные взносы в банк в размере 4 тыс. грн.
Необходимо определить размер процентной ставки при условии, что взносы и начисление на них процентов производится в конце года.
Прежде всего определим коэффициент наращения ренты, который равняется : .
По финансовым таблицам находим ближайшие значения факторного множителя: и .
Для расчета процентной ставки по методу линейной интерполяции используется формула:
где нижнее и верхнее значение предполагаемой процентной
ставки;
значения коэффициентов наращения при использовании процентных ставок и .
Для условий нашего примера значение процентной ставки, обеспечивающей за указанный срок создание резервного фонда в заданном объеме рассчитывается по формуле:
или 15,09%.
Оценка постоянного аннуитета пренумерандо.
Если на денежные поступления начисляются только сложные проценты, то соответствующие расчетные формулы для наращенных сумм аннуитета пренумерандо легко можно вывести из ранее рассмотренных формул для аннуитета постнумерандо.
Поскольку денежные поступления в аннуитете пренумерандо происходят в начале каждого периода, то этот аннуитет отличается от аннуитета постнумерандо только количеством периодов начисления процентов.
Например, для срочного аннуитета пренумерандо с регулярными денежными поступлениями А и процентной ставкой r , наращенный денежный поток имеет вид:
Следовательно, будущая стоимость аннуитета пренумерандо может быть определена по формуле:
Т.е. наращенная стоимость аннуитета пренумерандо больше в раз наращенной суммы аннуитета постнумерандо.
Аналогичным образом можно получить формулы для определения будущей стоимости аннуитета пренумерандо с начислением процентов m раз в течение базового периода и для р-срочных аннуитетов:
Несколько иной будет ситуация в р-срочном аннуитете пренумерандо, когда на взносы, поступающие в течение базового периода, начисляются простые проценты.
В отличие от аннуитета постнумерандо в этом аннуитете в каждом периоде любой взнос «действует» еще 1/р –ю часть периода, тем самым доставляя к концу периода дополнительную величину .
Следовательно, к концу каждого периода взносы, число которых равно р , доставят величину
Таким образом, на последнее р-е поступление начисляются простые проценты за часть периода, равную 1/р , и оно будет равно предпоследнее (р – 1)-е поступление станет равным и т.д. вплоть до первого поступления, которое станет равным . Следовательно, сумма этих величин, образующих арифметическую прогрессию, равна:
Таким образом, будущая стоимость аннуитета пренумерандо будет равняться:
В случае начисления только сложных процентов формулы для расчетов приведенных стоимостей пренумерандо имеют вид, аналогичный ранее полученным для аннуитета постнумерандо:
Из приведенных формул понятно, почему в финансовых таблицах не уточняется, какая схема подразумевается в финансовой сделке – постнумерандо или пренумерандо. Содержание таблиц инвариантно к этому фактору. Однако, при применении расчетных формул или финансовых таблиц необходимо строго следить за схемой поступления денежных платежей.
Пример.
Ежегодно в начале года в банк делается очередной взнос в размере 10 тыс. грн. Банк платит 20% годовых.
Какая сумма будет на счете по истечении трех лет?
тыс. грн.
Многие практические задачи могут быть решены различными способами в зависимости от того, какой денежный поток выделен аналитиком. Рассмотрим это на следующем примере.
Пример.
Вам предложено инвестировать 100 тыс. грн. на срок 5 лет при условии возврата этой суммы частями ежегодно по 20 тыс. грн. По истечении 5 лет выплачивается дополнительное вознаграждение в размере 30 тыс. грн.
Следует ли принимать это предложение, если можно депонировать деньги в банк из расчета 12% годовых?
Наращенная сумма депонирования:
тыс. грн.
В отношении альтернативного варианта, предусматривающего возмещение вложенной суммы частями, предполагается, что ежегодные поступления в размере 20 тыс. грн. можно немедленно пускать в оборот, получая дополнительные доходы. Если нет других альтернатив по эффективному использованию этих сумм, их можно депонировать в банк. В этом случае денежный поток можно представить двояко:
а) как срочный аннуитет постнумерандо с параметрами: А= 20,
n = 5, r = 20% и единовременное получение 30 тыс. грн. в конце периода:
тыс. грн.
б) как срочный аннуитет пренумерандо с параметрами: А = 20,
n = 4, r = 20% и единовременное получение сумм в 30 и 20 тыс. грн. в конце финансовой операции:
тыс. грн.
Таким образом, предложение экономически нецелесообразно.
Бессрочный аннуитет.
Аннуитет считается бессрочным, если денежные поступления продолжаются достаточно длительное время. Математически это означает, что . Характерным примером бессрочного аннуитета являются консоли – выпускаемые правительствами некоторых стран облигации, по которым производят регулярные купонные выплаты, но которые не имеют фиксированного срока. В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет. Бессрочный аннуитет также называют вечной рентой.
Определение будущей стоимости бессрочного аннуитета, естественно, не имеет смысла. Что же касается обратной задачи (определение приведенной стоимости), то она имеет вполне определенное решение.
Поток платежей в постоянном бессрочном аннитете при одном денежном поступлении А за период, являющися базовым для начисления процентов по ставке r, представляет собой бесконечно убывающую геометрическую прогрессию с первым членом и знаменателем . Для бессрочного аннуитета постнумерандо формула для определения приведенной стоимости имеет вид:
где
Приведенная формула показывает, что поток даже с неограниченным числом платежей имеет все же конечную приведенную стоимость. С финансовой точки зрения это вполне понятно, поскольку деньги, которые поступят через много лет, сейчас мало что стоят, а при высокой инфляции и ничего не стоят. Эта же ситуация проявляется и при сравнении коэффициентов дисконтирования бессрочного аннуитета и аннуитетов с большим сроком Для сравнения приведем в таблице значения FM4(r,n) при r = 10%.
Cрок аннуитета
40
50
60
70
90
∞
FM4(r = 10%,n)
9,7791
9,9148
9,9672
9,9873
9,9981
10
Из приведенной таблицы видно, что при сроке аннуитета, превышающем 50 лет, коэффициенты дисконтирования аннуитета незначительно отличаются друг от друга.
Кроме того, с ростом процентной ставки величина срока, начиная с которого величина факторного множителя FM4(r,n) перестают сильно отличаться друг от друга, уменьшается. Например, при r = 15% такой срок равняется 40 годам. Таким образом, при больших сроках аннуитета и большом уровне процентной ставки для определения приведенной стоимости срочного аннуитета можно воспользоваться формулой для определения приведенной стоимости бессрочного аннуитета, при этом полученный приблизительный результат будет не слишком отличаться от точного значения.
Приведенная формула используется для оценки целесообразности приобретения бессрочного аннуитета, если известен размер денежного поступления за период. В качестве r обычно принимается гарантированная процентная ставка, например, предлагаемая государственным банком.
Пример.
Необходимо определить текущую стоимость бессрочного аннуитета постнумерандо с ежегодным поступлением 4,2 тыс. грн., если предлагаемый государственным банком процент по срочным вкладам равен 14% годовых.
тыс. грн.
Следовательно, если аннуитет предлагается по цене, не превышающей 30 тыс. грн., то инвестирование в него будет представлять выгодную для инвестора операцию.
С помощью вышеприведенной формулы можно определить истинную стоимость обыкновенной акции в том случае, когда выплачиваются одинаковые дивиденды (равные А) в течение всего времени финансовой операции. При этом предположении темп ростов дивидендов равен нулю и соответствующая модель называется моделью нулевого роста.
Такая ситуация в определенном смысле свойственна привилегированным акциям высокого качества, выплаты дивидендов по которым одинаковы, регулярны и не зависят от величины прибыли на одну акцию, а время обращения привилегированных акций не ограничено.
Пример.
Компания гарантирует выплату дивидендов в размере 6 тыс. грн. на акцию в конце каждого года в течение неопределенно долгого времени.
Имеет ли смысл покупать акции этой компании в течение неопределенно долгого времени по цене 35 тыс. грн., если можно поместить деньги на депозит под 15% годовых?
Из формулы тыс. грн. следует, что истинная стоимость акции составляет 40 тыс. грн. Следовательно, это предложение может быть принято и акции компании можно приобретать.
Приведенная стоимость бессрочного аннуитета постнумерандо с денежными поступлениями р раз за базовый период и начислением сложных процентов m — раз за период может быть получена из следующей формулы:
Пример.
Фирма собирается учредить фонд для ежегодной (в конце года) выплаты пособий своим работникам.
Необходимо определить сумму, которую фирма должна поместить на депозит в банк, чтобы обеспечить получение неограниченно долго в конце каждого года 8 тыс. грн., если банк начисляет:
а) ежегодно сложные проценты по ставке 16%;
б) ежеквартально сложные проценты по ставке 14%;
в) непрерывные проценты с силой роста 13,5%.
Во всех трех случаях денежный поток является бессрочным аннуитетом постнумерандо. Необходимо найти приведенную стоимость такого аннуитета.
а) тыс. грн.
б) тыс. грн.
в) тыс. грн.
Приведенная стоимость бессрочного аннуитета пренумерандо в общем виде определяется с помощью приведенной стоимости бессрочного аннуитета постнумерандо по следующей формуле:
Следовательно, приведенная стоимость бессрочного аннуитета пренумерандо отличается от таковой для аннуитета постнумерандо на величину первого платежа.
Непрерывный аннуитет.
Предположим, что в течение каждого периода времени денежные поступления происходят очень часто, так что промежутки между последовательными поступлениями представляют собой бесконечно малые величины.
В этом случае аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью: одно и то же количество денежных единиц в единицу времени.
Соотношения, характеризующие непрерывный аннуитет, можно вывести из формул для р-срочного аннуитета, переходя в них к пределу при и несколько модифицируя величину члена аннуитета.
Ясно, что непрерывно не может поступать величина А, так как через любой малый промежуток времени накопится бесконечно большая сумма денег.
Пусть в конце каждого периода р-срочного аннуитета суммарная величина денежных поступлений составит , тогда каждое поступление будет равняться и ранее рассмотренная формула может быть использована для оценки будущей стоимости непрерывного аннуитета:
Приведенная стоимость непрерывного аннуитета рассчитывается по формуле:
Пример.
В течение 6 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя 40 тыс. грн.
Определить сумму, накопленную к концу шестого года при использовании процентной ставки 12% годовых.
Считая, что платежи поступают непрерывным образом, рассчитаем будущую стоимость непрерывного аннуитета:
тыс. грн.
Эта же задача может быть решена иначе, если примем р = 360, а А = 40/360:
тыс. грн.
Выполнив расчет видим, что результаты вычислений по двум формулам привели практически к одинаковому результату.
Если проценты начисляются раз за период, то пользуются формулой:
Аннуитет с изменяющейся величиной платежа.
На практике возможны ситуации, когда величина платежа меняется со временем в сторону увеличения или уменьшения. Например, при заключении договора аренды в условиях инфляции может предусматриваться периодическое увеличение платежа, компенсирующее негативное влияние изменения цен. Или другой пример, когда величина амортизационных отчислений может меняться в связи с изменением количества и стоимости основных фондов.
В таких ситуациях поток платежей представляет собой переменный аннуитет (переменную ренту) и для определения будущей или приведенной стоимости необходимо пользоваться ранее рассмотренными формулами для переменного аннуитета. Однако, когда члены аннуитета изменяются в соответствии с некоторыми законами, эти формулы существенно могут быть упрощены.
Предположим, что имеется аннуитет постнумерандо, платежи которого образуют арифметическую прогрессию с первым членом А и разностью z.
В этом случае говорят о переменном аннуитете с постоянным абсолютным изменением его членов. Если число периодов равно n, а r является процентной ставкой за базовый период, в соответствии с которой один раз в конце периода начисляются сложные проценты и период аннуитета совпадает с базовым, то наращенный денежный поток, записанный в порядке поступления платежей имеет вид:
Если z >0, то члены аннуитета возрастают. Если z <0, члены аннуитета убывают и число этих членов должно удовлетворять равенству n < 1 – A/z, иначе можно получить отрицательные платежи, что лишено смысла.
Сложив наращенные члены аннуитета и сгруппировав отдельно слагаемые, содержащие множители А и z, получим:
Из этого выражения с помощью определенных преобразований получаем формулы для определения будущей и приведенной стоимости такого аннуитета:
Пример.
Согласно условиям финансового соглашения на счет в банке в течение 6 лет в конце года будут поступать денежные суммы, первая из которых равна 5 тыс. грн., а каждая последующая будет увеличиваться на 0,4 тыс. грн.
Необходимо оценить аннуитет, если банк применяет процентную ставку 10% годовых и сложные проценты начисляются один раз в конце года.
Как изменятся оценки аннуитета, если денежные суммы будут уменьшаться на 0,4 тыс. грн.?
а) для условия возрастания членов аннуитета:
тыс.грн.
тыс. грн.
б) для условия уменьшения членов аннуитета:
тыс. грн.
тыс. грн.
Для оценки аннуитетов пренумерандо используются следующие формулы:
Аналогичным образом можно получить оценки аннуитета для других ситуаций, например, для случая, если в указанных выше условиях начисление сложных процентов происходит раз за базовый период:
Пример.
В условиях предыдущего примера определить будущую стоимость аннуитета, если начисление сложных процентов происходит в конце каждого полугодия.
тыс.грн.
Из формул для определения будущей и приведенной стоимости аннуитета можно определить величину аннуитета А и разность z:
Что касается процентной ставки и продолжительности аннуитета, то формулы для их определения в явном виде не могут быть получены. Поэтому для определения этих параметров используются приближенные методы.
Пример.
За 10 лет необходимо накопить 60 тыс. грн. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 300 грн. и процентная ставка равна 15% годовых? Денежные поступления и начисление сложных процентов осуществляются в конце года.
Определить, на какую величину необходимо увеличивать каждый год денежное поступление, если первый вклад будет равен 2,5 тыс. грн.?
тыс.грн.
тыс. грн.
Предположим, что платежи в аннуитете образуют геометрическую прогрессию с первым членом А и знаменателем q.
В этом случае имеет место переменный аннуитет с постоянным относительным изменением его членов.
Если r является процентной ставкой за базовый периолд, совпадающий с периодом аннуитета, n равно числу периодов и в конце каждого периода начисляются сложные проценты, то наращенный денежный поток имеет вид:
Представленная последовательность чисел представляет собой геометрическую прогрессию с первым членом и знаменателем . Поэтому будущая стоимость такого аннуитета будет равна:
Приведенная стоимость аннуитета определяется по формуле:
Пример.
По условиям контракта на счет в банке поступают в течение 5 лет в конце года платежи. Первый платеж равен 3 тыс. грн., а каждый следующий год по отношению к предыдущему увеличивается на 15%
Необходимо оценить такой аннуитет, если банк начисляет в конце каждого года сложные проценты из расчета 12% годовых.
Увеличение платежа на 15% означает его рост в1,15 раза, т.е. поток платежей образует геометрическую прогрессию с знаменателем q =1,15.
тыс. грн.
тыс. грн.
Используя вышеприведенные формулы для расчета будущей и приведенной стоимости аннуитета можно напистаь в явном виде формулы для определения только величины аннуитета:
Что касается знаменателя геометрической прогрессии, процентной ставки и продолжительности аннуитета, то эти параметры могут быть определены только с помощью приближенных методов.
Если же члены переменного аннуитета не образуют ни арифметическую, ни геометрическую прогрессию, то, тем не менее, во многих случаях оценка таких аннуитетов может быть выполнена с помощью финансовых таблиц. Рассмотрим технику подобных вычислений на следующем примере.
Пример.
Садовый участок сдается в аренду на 10 лет. Арендная плата будет осуществляться ежегодно по схеме постнумерандо на следующих условиях: в первые шесть лет – по 10 тыс. грн., а в оставшиеся четыре года – по 11 тыс. грн.
Требуется оценить приведенную стоимость этого договора, если процентная ставка, используемая аналитиком, равна 15%.
Решать данную задачу можно различными способами, в зависимости от того, какие аннуитеты будут выделены аналитиком.
Ествественн, приведенная стоимость денежного потока должна оцениваться с позиции начала первого временного интервала.
Рассмотрим два возможных варианта. Оба варианта основываются на свойстве аддитивности рассмотренных алгоритмов в отношении величины аннуитетного платежа.
1) Исходный поток можно представить как сумму двух аннуитетов: первый имеет А = 10 тыс. грн. и продолжается 10 лет, второй имеет А = 1 тыс. грн. и продолжается четыре года.
По формуле оцениваем приведенную стоимость каждого аннуитета. Однако второй аннуитет в этом случае будет оценен с позиции начала седьмого года. Поэтоому полученную сумму необходимо дисконтировать с помощью формулы к началу первого года. В этом случае оценки двух аннуитетов будут приведены к одному моменту времени, а их сумма даст оценку приведенной стоимости исходного денежного потока:
тыс. грн.
2) Исходный поток можно представить как разность двух аннуитетов: первый имеет А = 11 тыс. грн. и продолжается десять лет; второй имеет А = 1 тыс. грн. и, начавшись в первом году, заканчивается в шестом. В этом случае расчет выглядит так:
тыс. грн.
Аннуитеты с периодом, большим, чем базовый.
Ранее были рассмотрены аннуитеты, периоды которых не превосходили базовые периоды начисления процентов. В частности, мы говлрили, что если базовый период равен году, то период аннуитета не превышал одного года. Однако, в финансовых операциях бывают случаи срочных аннуитетов, у которых их период больше года. Предположим, речь идет о срочном аннуитете с денеежными поступлениями каждые два года.
Предположим есть постоянный аннуитет постнумерандо, денежные поступления которого каждое в размере А происходят в течение n периодов, являющихся базовым для начисления процентов по ставке r. Причем денежные поступления происходят каждые u периодов, а начисление сложных процентов – в конце каждого периода. Оценим будущую стоимость аннуитета.
Последнее поступление равняется А. На предпоследнее поступление начисляются сложные проценты за u периодов и оно будет равно . На поступление начисляютя сложные проценты за 2u периодов и оно будет равно и т.д. до первого включительно, которое равняется
Полученные величины образуют геометрическую прогрессию с первым членом А, знаменателем и числом членов, равным u. Поэтому сумма этих величин будет равна:
Пример.
Работник заключает с фирмой пенсионный контракт на 10 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет поступать 1,4 тыс. грн.
Требуется определить наращенную к концу действия контракта сумму, если на денежные поступления будут ежегодно начисляться декурсивные сложные проценты по ставке 12% годовых.
В соответствии с контрактом денежные суммы образуют аннуитет длительностью 10 лет и периодом 2 года. Т.о. период аннуитета больше базового периода начисления процентов.
тыс. грн.
Если начисление сложных процентов происходит раз m в течение этого периода, то для нахождения будущей стоимости аннуитета используется следующая формула:
Пример.
Фирма решила образовать фонд для обеспечения будущих расходов, связанных с реконструкцией производства. С этой целью в конце каждых трех лет фирма перечисляет в банк 8 тыс. грн.
Какая сумма будет на счете фирмы через 15 лет, если на поступающие суммы будут ежеквартально начисляться сложные проценты по номинальной годовой процентной ставке 16%?
тыс. грн.
Если начисление сложных процентов происходит раз за базовый период и необходимо найти приведенную стоимость будущих поступлений то используется формула:
Откуда:
«22. Магнитные усилители без обратной связи» — тут тоже много полезного для Вас.
Пример.
Определить сумму, которую необходимо поместить на счет в банке, чтобы в течение 8 лет в конце каждого двухлетнего периода иметь возможность снимать со счета 3 тыс. грн., причем к концу срока полностью выбрать все деньги со счета, если на находящиеся на счете денежные суммы будут начисляться каждые полгода сложные проценты по ставке 12% годовых.
тыс. грн.
Формулы для оценок аннуитета пренумерандо получаются из соответствующих формул для оценки аннуитета постнумерандо:
и
Аннуитет 2021
Поделиться видео // www. Investopedia. ком / термины / а / аннуитет. aspЧто такое «Аннуитет»
Аннуитет — это контрактный финансовый продукт, продаваемый финансовыми учреждениями, который предназначен для приема и увеличения средств от физического лица, а затем, после аннуитизации, выплачивать поток платежей физическому лицу в более позднем пункте во время. Период времени, когда аннуитет финансируется и до начала выплаты, называется фазой накопления. Как только платежи начинаются, контракт находится на стадии аннулирования.
РАЗВЛЕЧЕНИЕ «Аннуитет»
Аннуитеты были разработаны, чтобы быть надежным средством обеспечения устойчивого денежного потока для отдельного лица в течение их лет выхода на пенсию, а также для облегчения опасений относительно риска долголетия или изживающих свои активы ,
Аннуитеты также могут быть созданы, чтобы превратить значительную паушальную сумму в устойчивый денежный поток, например, для победителей крупных денежных расчетов по иску или выиграть в лотерею.
Пенсии с установленными выплатами и социальное обеспечение — это два примера гарантированных пожизненными аннуитетами, которые платят пенсионерам устойчивый денежный поток до тех пор, пока они не пройдут.
Типы аннуитетов
Аннуитеты могут быть структурированы в соответствии с широким спектром деталей и факторов, таких как продолжительность времени, в течение которого платежи от аннуитета могут быть гарантированы. Аннуитеты могут быть созданы таким образом, чтобы при аннуитизации платежи продолжались до тех пор, пока не будет погашен либо аннуитет, ни их супруг (если выбор на выживание). В качестве альтернативы, аннуитеты могут быть структурированы для выплаты средств в течение фиксированного периода времени, например 20 лет, независимо от того, как долго проживает аннуитет. Кроме того, аннуитеты могут начинаться сразу же после внесения единовременной суммы, или они могут быть структурированы как отсроченные выгоды.
Аннуитеты могут быть структурированы как фиксированные, так и переменные. Фиксированные аннуитеты предоставляют регулярные периодические платежи аннуитету. Переменные аннуитеты позволяют владельцу получать большие будущие денежные потоки, если инвестиции в фонд аннуитета преуспевают и уменьшают платежи, если его инвестиции идут плохо. Это обеспечивает менее стабильный денежный поток, чем фиксированный аннуитет, но позволяет аннуитету пожинать плоды прибыли от инвестиций своего фонда.
Одна критика аннуитетов заключается в том, что они неликвидны. Депозиты в аннуитетные контракты обычно запираются на определенный период времени, известный как период сдачи, когда аннуитету будет нанесен штраф, если все или часть этих денег будут затронуты. Эти периоды сдачи могут составлять от 2 до более 10 лет, в зависимости от конкретного продукта. Сборы за сдачу могут начинаться с 10% и более, и штраф обычно снижается ежегодно в течение периода сдачи.
В то время как переменные аннуитеты несут некоторый рыночный риск, и потенциал потерять основной, гонщики и функции могут быть добавлены к аннуитетным контрактам (как правило, за дополнительную плату), которые позволяют им функционировать как аннуитеты с фиксированной переменной.Владельцы контрактов могут воспользоваться потенциалом роста портфеля, сохраняя при этом гарантированную гарантированную максимальную выгоду при снижении стоимости, если стоимость портфеля снижается. Другие гонщики могут быть приобретены, чтобы добавить смертельную выгоду в контракт или ускорить выплаты, если у владельца аннуитета диагностирована терминальная болезнь. Стоимость проживающих всадников является общей для корректировки годовых базовых денежных потоков для инфляции на основе изменений в ИПЦ.
Кто продает аннуитеты
Компании по страхованию жизни и инвестиционные компании — это два вида финансовых учреждений, предлагающих продукты аннуитета. Для компаний, занимающихся страхованием жизни, аннуитеты являются естественным хеджем для своих страховых продуктов. Страхование жизни приобретается для борьбы с риском смертности, то есть с риском смерти преждевременно. Страхователи выплачивают ежегодную премию страховой компании, которая выплачивает единовременную сумму после их смерти. Если страхователи преждевременно умирают, страховщик выплачивает выплату пособия в связи с потерей прибыли в результате чистых убытков компании. Опыт актуарной науки и претензий позволяет этим страховым компаниям оценивать свою политику, чтобы в среднем страховые покупатели жили достаточно долго, чтобы страховщик получал прибыль. С другой стороны, аннуитеты имеют дело с риском долговечности или с риском изживающих себя активов. Риск для эмитента аннуитета заключается в том, что владельцы аннуитетов будут жить в своих первоначальных инвестициях. Эмитенты аннуитетов могут хеджировать риск долголетия, продавая аннуитеты клиентам с более высоким риском преждевременной смерти.
Во многих случаях денежная стоимость в рамках постоянных полисов страхования жизни может быть обменена посредством обмена 1035 на аннуитетный продукт без каких-либо налоговых последствий.
Агенты или брокеры, продающие аннуитеты, должны иметь государственную лицензию на страхование жизни, а также лицензию на ценные бумаги в случае переменных аннуитетов. Эти агенты или брокеры обычно получают комиссию, основанную на условной стоимости аннуитетного контракта.
Кто покупает аннуитеты
Аннуитеты — это подходящие финансовые продукты для физических лиц, которые ищут стабильный, гарантированный пенсионный доход. Поскольку единовременная сумма, внесенная в аннуитет, является неликвидной и подлежит штрафам за взыскание, она не рекомендуется для молодых людей или для лиц с ограниченными физическими возможностями. Держатели аннуитетов не могут пережить свой поток дохода, который хеджирует риск долголетия. До тех пор, пока покупатель понимает, что он или она торгует жидкой единовременной суммой за гарантированную серию денежных потоков, продукт подходит. Некоторые покупатели надеются выдать аннуитет в будущем с прибылью, однако это не намеренное использование продукта.
Непосредственные аннуитеты часто покупаются людьми любого возраста, которые получили большую кучу денег и предпочитают обменять его на денежные потоки в будущем. Проклятие победителя лотереи заключается в том, что многие победители лотереи, которые берут кучу денег, часто тратят все эти деньги за относительно короткий период времени.
Разница между обычным аннуитетом и аннуитетом
Аннуитет описывается как поток фиксированных денежных потоков, то есть платежей или поступлений, которые происходят периодически, с течением времени. Например, оплата жилищного кредита, премии по страхованию жизни, арендной платы и т. Д. Может быть двух видов аннуитетов, то есть обычный аннуитет и аннуитет. Обычный аннуитет означает аннуитет, который относится к периоду, предшествующему его дате, а аннуитет — аннуитет, относящийся к периоду, следующему за его датой.Большинство людей используют аннуитет в качестве пенсионного инструмента (пенсии), который гарантирует стабильный доход в ближайшие годы. Равная сумма должна быть выплачена или получена в качестве аннуитета, и временной интервал между последовательными платежами должен быть одинаковым.
Существует разница между обычным аннуитетом и аннуитетом, который заключается в сроках двух аннуитетов. Итак, в статье делается попытка пролить свет на различия между двумя взглядами.
Сравнительная таблица
Основа для сравнения Обычный аннуитет Ежегодный взнос Имея в виду Обычный аннуитет — это тот, в котором приток или отток денежных средств подлежат оплате в конце каждого периода. Аннуитетный платеж описывается как последовательность денежных потоков, возникающих в начале каждого периода. Оплата Относится к периоду, предшествующему его дате. Принадлежит к периоду после его даты. Подходит для платежи поступления пример Жилищный кредит, оплата ипотеки, купонных облигаций и др. Арендные платежи, страховые взносы и т. Д. Определение обычного аннуитета
Обычный аннуитет определяется как ряд регулярных платежей или поступлений; это происходит через регулярные промежутки времени в течение определенного количества периодов. — (n-1) / r)
где PMT = период оплаты наличными
r = процентная ставка за период
n = общее количество периодов
Ключевые различия между обычным аннуитетом и аннуитетом
Приведенные ниже пункты заслуживают внимания, поскольку речь идет о разнице между обычным аннуитетом и причитающимся аннуитетом:
- Обычный аннуитет относится к последовательности постоянного денежного потока, платеж которого должен быть произведен или получен в конце каждого периода. Аннуитетный платеж подразумевает поток платежей или поступлений, которые подлежат оплате в начале каждого периода.
- Каждый приток или отток обычного аннуитета связан с периодом, предшествующим его дате. Напротив, аннуитетный платеж представляет собой период движения денежных средств, следующий за его датой. Поскольку денежные потоки, причитающиеся аннуитету, происходят на один период раньше, чем у обычного аннуитета.
- Обычный аннуитет лучше всего, когда человек делает платеж, тогда как причитающийся аннуитет уместен, когда человек собирает платеж. Поскольку платеж, произведенный по аннуитету, имеет более высокую приведенную стоимость, чем обычный аннуитет. Это из-за принципа временной стоимости денег, то есть стоимость одной рупии, сегодня больше, чем стоимость одной рупии, после одного года.
- Выплата автокредита, оплата ипотечных и купонных облигаций — вот несколько примеров обычной аннуитета. С другой стороны, распространенными примерами аннуитетного платежа являются арендные платежи, оплата автомобилей, выплата страховых взносов и т. Д.
Заключение
Аннуитет направлен на обеспечение постоянного потока дохода для владельца аннуитета в течение длительного времени. Человек может сделать выбор между этими двумя аннуитетами, учитывая некоторые факторы, такие как доход, который он хочет получить при выходе на пенсию, и степень риска, на которую он может пойти.
Временная стоимость денег — Совет по уравнению
На этом уроке обсуждаются аннуитеты в контексте функций сложных процентов, представленных в Справочник оценщика Раздел 505 (AH 505), Формулы капитализации и таблицы . Урок:
- Определяет аннуитет и два типа аннуитета,
- Объясняет, как преобразовать коэффициент обычной ренты в соответствующий коэффициент выплаты ренты, и
- Содержит примеры преобразования коэффициентов ренты.
Определение аннуитета
Аннуитет — это серия равных денежных потоков или платежей, осуществляемых через регулярные промежутки времени. (например, ежемесячно или ежегодно). Выплаты должны быть равными, а интервалы между выплатами должны быть регулярными.
Следующие функции сложных процентов в AH 505 включают аннуитеты:
Существует два типа аннуитетов:- Обычная рента
- Аннуитетный платеж
Обыкновенная рента
Обычный аннуитет — это аннуитет, в котором денежные потоки или платежи происходят в конце периода.
Обычный аннуитет денежных поступлений в размере 100 долларов США в год в течение 5 лет может быть представлен следующим образом:
Денежные потоки возникают в конце 1-5 годов. И первый денежный поток происходит в конце 1-го года.
Большинство проблем с оценкой связаны с обычными аннуитетами; то есть платежи предполагаются в конце периода. Все формулы и коэффициенты в 505 хиджры относятся только к обычным аннуитетам.
Аннуитетный платеж
Аннуитет к оплате — это аннуитет, в котором денежные потоки или платежи происходят в начале периода. Аннуитет также называется аннуитетом за просрочку.
Аннуитет при поступлении денежных средств в размере 100 долларов США в год в течение 5 лет может быть представлен следующим образом:
Денежные потоки возникают в начале лет с 1 по 5. И первый денежный поток происходит в момент времени 0 (сейчас).
Практические приложения Преобразование коэффициентов ренты
Как уже отмечалось, большинство проблем с оценкой предполагает, что выплаты происходят в конце периода (обычный аннуитет). Но если платежи происходят в начале периода (причитающийся аннуитет), обычный коэффициент аннуитета в 505 хиджры может быть преобразован в соответствующий ему коэффициент аннуитета с относительно простым расчетом.
Хотя финансовые калькуляторы и программное обеспечение для работы с электронными таблицами еще больше упрощают преобразование обычного аннуитета в подлежащий выплате аннуитет, полезно понять, как «вручную» преобразовать коэффициенты обычного аннуитета в 505 хиджры в коэффициенты причитающегося аннуитета.
Преобразование коэффициента обычной аннуитета в коэффициент выплаты аннуитета для FW $ 1 / P или PW $ 1 / P :
Для определения будущей стоимости периода в 1 доллар ( FW 1 / P ) или текущей стоимости периода в 1 доллар ( PW 1 / P ) коэффициент для причитающегося аннуитета, см. соответствующий коэффициент в AH 505 для обычного аннуитета и умножьте на коэффициент (1 + периодическая процентная ставка).
Периодическая ставка будет отличаться в зависимости от интервала начисления сложных процентов в задаче. Например, при ежегодном начислении сложных процентов периодическая ставка будет такой же, как и годовая ставка; с ежемесячным начислением сложных процентов периодическая ставка будет равна годовой ставке, деленной на 12.
Пример 1: Преобразование в коэффициент выплаты аннуитета для FW $ 1 / P
Рассчитайте коэффициент FW $ 1 / P на 4 года при годовой процентной ставке 6% с годовой начисление сложных процентов при условии, что выплаты производятся в начале каждого года.Решение:
При ежегодном начислении сложных процентов периодическая ставка равна годовой ставке (6 процентов, или 0,06).- Фактор выплаты аннуитета = Фактор обычного аннуитета (в 505 хиджры, стр. 33) × (1 + периодическая ставка)
- Коэффициент выплаты аннуитета = 4,374616 × (1 + 0,06)
- Коэффициент выплаты аннуитета = 4,637093
Пример 2: Преобразование в коэффициент уплаты аннуитета для PW $ 1 / P
Рассчитайте коэффициент PW $ 1 / P на 4 года при годовой процентной ставке 6% с ежемесячно начисление сложных процентов при условии, что выплаты производятся в начале каждого месяца.Решение:
При ежемесячном начислении сложных процентов периодическая ставка составляет 6% ÷ 12 = половина одного процента в месяц или 0,06 ÷ 12 = 0,005.- Фактор выплаты аннуитета = Фактор обычного аннуитета (в 505 хиджры, стр.32) × (1 + периодическая ставка)
- Коэффициент погашения аннуитета = 42,580318 × (1 + 0,005) Коэффициент выплаты аннуитета
- = 42.793220
Преобразование коэффициента обычной ренты в коэффициент выплаты ренты для SFF или PR :
Чтобы определить коэффициент фонда погашения ( SFF ) или коэффициент периодического погашения ( PR ) для причитающегося аннуитета, см. соответствующий коэффициент в 505 хиджры для обычного аннуитета, и разделите его на на коэффициент (1+ периодическая процентная ставка).При преобразовании коэффициентов SFF и PR обязательно делите, а не умножайте. Примечание: периодическая ставка будет отличаться в зависимости от интервала начисления сложных процентов в задаче.
Пример 3: Преобразование в аннуитет для SFF
Рассчитайте SFF на 4 года с годовой процентной ставкой 6% с ежегодным начислением сложных процентов, предполагая, что платежи происходят в начале каждого года.Решение:
Пример 4: Преобразование в аннуитет для PR
Рассчитайте коэффициент PR на 4 года при годовой процентной ставке 6% с ежемесячным начислением сложных процентов, предполагая, что платежи происходят в начале каждого месяца (коэффициент ежемесячного аннуитета).Решение:
Обзор, виды и формулы для оценки аннуитета
Что такое аннуитет?
Аннуитет — это финансовый продукт, который обеспечивает определенные денежные потоки. Денежный поток. Денежный поток (CF) — это увеличение или уменьшение денежной суммы, имеющейся у компании, учреждения или физического лица. В финансах этот термин используется для описания суммы наличных денег (валюты), которые генерируются или потребляются в определенный период времени.Есть много типов CF через равные промежутки времени. Аннуитеты создаются финансовыми учреждениями Группа финансовых институтов (FIG) Группа финансовых институтов (FIG) — это группа профессионалов, которые предоставляют консультационные услуги финансовым учреждениям. Некоторые из услуг, которые предлагает FIG, включают слияния и поглощения, рекапитализацию, привлечение капитала, финансовую реструктуризацию, корпоративную оценку, экспертные финансовые заключения и другие консультационные услуги, в первую очередь компаниям по страхованию жизни, для обеспечения регулярного дохода для клиента.
Аннуитет является разумной альтернативой некоторым другим инвестициям в качестве источника дохода, поскольку он обеспечивает гарантированный доход физическому лицу. Однако аннуитеты менее ликвидны, чем инвестиции в ценные бумаги. Ценные бумаги с фиксированным доходом. Ценные бумаги с фиксированным доходом — это тип долгового инструмента, который обеспечивает возврат в виде регулярных или фиксированных процентных выплат и погашений, поскольку первоначально внесенная единовременная сумма не может быть снята без штрафных санкций.
При выдаче аннуитета физическое лицо выплачивает единовременную сумму эмитенту аннуитета (финансовому учреждению). Затем эмитент удерживает сумму в течение определенного периода (называемого периодом накопления). По истечении периода накопления эмитент должен производить фиксированные платежи физическому лицу в соответствии с заранее определенными временными интервалами.
Аннуитеты в основном покупают люди, которые хотят получать стабильный пенсионный доход.
Типы аннуитетов
Существует несколько типов аннуитетов, которые классифицируются по частоте и типам платежей.Например, денежные потоки аннуитетов могут выплачиваться в разные промежутки времени. Выплаты могут производиться еженедельно, раз в две недели или ежемесячно. Основными видами аннуитетов являются:
1. Фиксированные аннуитеты
Аннуитеты, обеспечивающие фиксированные выплаты. Платежи гарантированы, но доходность обычно минимальна.
2. Изменяемые аннуитеты
Аннуитеты, которые позволяют физическому лицу выбрать набор инвестиций, по которым будет выплачиваться доход в зависимости от эффективности выбранных инвестиций.Переменные аннуитеты не гарантируют размер дохода, но норма прибыли, как правило, выше по сравнению с фиксированными аннуитетами.
3. Пожизненные аннуитеты
Пожизненные аннуитеты обеспечивают фиксированные выплаты их держателям до его / ее смерти.
4. Бессрочный
Аннуитет, который обеспечивает бессрочные денежные потоки без даты окончания. Примеры финансовых инструментов, которые предоставляют бессрочные денежные потоки своему держателю, крайне редки.
Наиболее ярким примером является облигация правительства Великобритании под названием consol.Первые консоли были выпущены в середине 18 -х годов века. Облигации не указывали точную дату окончания и подлежали погашению по усмотрению парламента. Однако правительство Великобритании выкупило все консоли в 2015 году.
Оценка аннуитетов
Аннуитеты оцениваются путем дисконтирования будущих денежных потоков аннуитетов и определения приведенной стоимости денежных потоков. Общая формула для оценки аннуитета:
Где:
- PV = Приведенная стоимость аннуитета
- P = Фиксированный платеж
- r = Процентная ставка
- n = Общее количество периодов аннуитетных платежей
Оценка бессрочных выплат отличается, поскольку она не включает указанную дату окончания.Таким образом, ценность бессрочного права определяется по следующей формуле:
PV =
P / rДополнительные ресурсы
CFI предлагает аналитику финансового моделирования и оценки (FMVA) ™ Стать сертифицированным специалистом по финансовому моделированию и оценке. Сертификат аналитика (FMVA) ® CFI по финансовому моделированию и оценке (FMVA) ® поможет вам обрести уверенность в своей финансовой карьере. Запишитесь сегодня! программа сертификации для тех, кто хочет вывести свою карьеру на новый уровень.Чтобы узнать больше о связанных темах, посетите следующие ресурсы CFI:
- Коммерческий страховой брокер Коммерческий страховой брокер Коммерческий страховой брокер — это физическое лицо, которому поручено действовать в качестве посредника между поставщиками страховых услуг и клиентами. Существование коммерческих страховых брокеров помогает клиентам не теряться в море надежных и недобросовестных страховых компаний.
- Федеральная корпорация по страхованию вкладов (FDIC) Федеральная корпорация по страхованию вкладов (FDIC) Федеральная корпорация по страхованию вкладов (FDIC) — это государственное учреждение, которое обеспечивает страхование вкладов от банкротства банка.Организация была создана
- Финансовый посредник Финансовый посредник Финансовый посредник — это учреждение, которое действует как посредник между двумя сторонами с целью облегчения финансовых транзакций. Учреждения, которые обычно называют финансовыми посредниками, включают коммерческие банки, инвестиционные банки, паевые инвестиционные фонды и пенсионные фонды.
- Ключевые игроки на рынках капитала Ключевые игроки на рынках капитала В этой статье мы даем общий обзор ключевых игроков и их соответствующих ролей на рынках капитала.Рынки капитала состоят из двух типов рынков: первичных и вторичных. Это руководство предоставит обзор всех крупных компаний и профессий на рынках капитала.
Расчет настоящей и будущей стоимости аннуитетов
У большинства из нас был опыт совершения серии фиксированных платежей в течение определенного периода времени, таких как аренда или оплата автомобиля, или получение серии платежей в течение определенного периода времени, таких как проценты по облигации или депозитному сертификату ( КОМПАКТ ДИСК).Эти повторяющиеся или текущие платежи технически называются «аннуитетами» (не путать с финансовым продуктом, называемым аннуитетом, хотя они взаимосвязаны).
Есть несколько способов измерить стоимость таких платежей или их конечную стоимость. Вот что вам нужно знать о расчете текущей стоимости (PV) или будущей стоимости (FV) аннуитета.
Ключевые выводы
- Периодические платежи, такие как арендная плата за квартиру или проценты по облигации, иногда называют «аннуитетами».«
- В обычных аннуитетах выплаты производятся в конце каждого периода. С причитающимися аннуитетами они выплачиваются в начале периода.
- Будущая стоимость аннуитета — это общая стоимость платежей в определенный момент времени.
- Текущая стоимость — это то, сколько денег потребовалось бы сейчас, чтобы произвести эти будущие платежи.
Два типа аннуитета
Аннуитеты в этом смысле слова подразделяются на два основных типа: обычные аннуитеты и аннуитеты, подлежащие уплате.
- Обычные аннуитеты : Обычные аннуитеты производят (или требуют) выплаты в конце каждого периода. Например, по облигациям обычно выплачиваются проценты в конце каждые шесть месяцев.
- Аннуитеты к уплате : При уплате аннуитета, напротив, выплаты производятся в начале каждого периода. Арендная плата, которую арендодатели обычно требуют в начале каждого месяца, является типичным примером.
Вы можете рассчитать текущую или будущую стоимость обычного или подлежащего выплате аннуитета, используя следующие формулы.
Расчет будущей стоимости обычной ренты
Будущая стоимость (FV) — это мера того, сколько будет стоить серия регулярных платежей в определенный момент в будущем при заданной процентной ставке. Так, например, если вы планируете инвестировать определенную сумму каждый месяц или год, он сообщит вам, сколько вы накопите на будущую дату. Если вы производите регулярные платежи по ссуде, будущая стоимость полезна для определения общей стоимости ссуды.
Рассмотрим, например, серию из пяти регулярных платежей по 1000 долларов.
Изображение Джули Банг © Investopedia 2019Из-за временной стоимости денег — концепции, согласно которой любая сумма сейчас стоит больше, чем она будет в будущем, потому что ее можно инвестировать тем временем, — первый платеж в 1000 долларов стоит больше, чем второй, и так далее. Итак, предположим, что вы инвестируете 1000 долларов каждый год в течение следующих пяти лет под 5% годовых. Ниже показано, сколько у вас будет в конце пятилетнего периода.
Изображение Джули Банг © Investopedia 2019Однако вместо того, чтобы рассчитывать каждый платеж по отдельности и затем складывать их все, вы можете использовать следующую формулу, которая скажет вам, сколько денег у вас будет в итоге:
FV Обычная рента знак равно C × [ ( 1 + я ) п — 1 я ] куда: C знак равно денежный поток за период я знак равно уровень интереса п знак равно количество платежей \ begin {align} & \ text {FV} _ {\ text {Обычная ~ рента}} = \ text {C} \ times \ left [\ frac {(1 + i) ^ n — 1} {i} \ right ] \\ & \ textbf {где:} \\ & \ text {C} = \ text {денежный поток за период} \\ & i = \ text {процентная ставка} \\ & n = \ text {количество платежей} \\ \ end {выровнен} FVОбычный аннуитет = C × [i (1 + i) n − 1], где: C = денежный поток за период; i = процентная ставка = количество платежей.
Используя приведенный выше пример, вот как это будет работать:
FV Обычная рента знак равно $ 1 , 0 0 0 × [ ( 1 + 0 .5 -1} {0,05} \ right] \\ & = \ 1000 $ \ times 5.53 \\ & = \ 5 525,63 $ \\ \ end {выровнено} FVОбычный аннуитет = 1000 долларов США × [0,05 (1 + 0,05) 5−1] = 1000 долларов США × 5,53 = 5 525,63 долларов США.
Обратите внимание, что разница в один цент в этих результатах — 5 525,64 доллара против 5 525,63 доллара — связана с округлением в первом расчете.
Расчет приведенной стоимости обыкновенной ренты
В отличие от расчета будущей стоимости, расчет приведенной стоимости (PV) показывает, сколько денег потребуется сейчас, чтобы произвести серию платежей в будущем, опять же с учетом установленной процентной ставки.
Вот как будет выглядеть расчет приведенной стоимости на том же примере с пятью платежами по 1000 долларов, сделанными в течение пяти лет. Он показывает, что 4 329,58 долларов, вложенных под 5% годовых, будет достаточно для осуществления этих пяти платежей по 1000 долларов. {-n}} {i } \ right] \\ \ end {выровнено} PV Обычная рента = C × [i1− (1 + i) −n]
Если мы подставим в уравнение те же числа, что и выше, вот результат:
PV Обычная рента знак равно $ 1 , 0 0 0 × [ 1 — ( 1 + 0 .{-5}} {0,05} \ right] \\ & = \ 1000 долларов \ times 4,33 \\ & = \ 4 329,48 долларов \\ \ end {выровнено} PV Обычный аннуитет = 1000 долларов США × [0,051− (1 + 0,05) −5] = 1000 долларов США × 4,33 = 4329,48 долларов США.
Расчет будущей стоимости аннуитета
Причитающийся аннуитет, как вы помните, отличается от обычного аннуитета тем, что платежи по причитающемуся аннуитету производятся в начале, а не в конце каждого периода.
Изображение Джули Банг © Investopedia 2019Для учета платежей, происходящих в начале каждого периода, требуется небольшая модификация формулы, используемой для расчета будущей стоимости обычного аннуитета, что приводит к более высоким значениям, как показано ниже. n — 1} {i} \ right] \ раз (1 + я) \\ \ конец {выровнено} FVAnnuity Due = C × [i (1 + i) n − 1] × (1 + i)
Здесь мы используем те же числа, что и в наших предыдущих примерах:
FV Ежегодный взнос знак равно $ 1 , 0 0 0 × [ ( 1 + 0 .5–1} {0,05} \ right] \ times (1 + 0,05) \\ & = \ 1000 $ \ times 5,53 \ times 1.05 \\ & = \ 5,801,91 $ \\ \ end {выровнено} FVAnnuity Due = 1000 долларов США × [0,05 (1 + 0,05) 5–1] × (1 + 0,05) = 1000 долларов США × 5,53 × 1,05 = 5 801,91 доллара США.
Опять же, обратите внимание, что разница в один цент в этих результатах, 5 801,92 доллара против 5 801,91 доллара, связана с округлением в первом расчете.
Расчет приведенной стоимости аннуитета
Точно так же формула для расчета приведенной стоимости аннуитета учитывает тот факт, что платежи производятся в начале, а не в конце каждого периода.
Например, вы можете использовать эту формулу для расчета приведенной стоимости ваших будущих арендных платежей, как указано в вашем договоре аренды. {-n}} {i} \ вправо] \ раз (1 + я) \\ \ конец {выровнено} PVAnnuity Due = C × [i1− (1 + i) −n] × (1 + i)
Итак, в этом примере:
PV Ежегодный взнос знак равно $ 1 , 0 0 0 × [ ( 1 — ( 1 + 0 .{-5}} {0,05} \ right] \ times (1 + 0,05) \\ & = \ 1000 $ \ times 4.33 \ times1.05 \\ & = \ 4545.95 $ \\ \ end {выровнено} PVAnnuity Due = 1000 долларов США × [0,05 (1– (1 + 0,05) −5] × (1 + 0,05) = 1000 долларов США × 4,33 × 1,05 = 4545,95 долларов США).
Текущая стоимость аннуитета
Итог
Формулы, описанные выше, позволяют — и относительно легко, если вы не возражаете против математики — определить текущую или будущую стоимость либо обычной ренты, либо подлежащей выплате ренты. Финансовые калькуляторы (вы можете найти их в Интернете) также могут рассчитать их за вас с правильными данными.
Определение обыкновенного аннуитета
Что такое обыкновенная рента?
Обычный аннуитет — это серия равных платежей, производимых в конце последовательных периодов в течение фиксированного периода времени. Хотя выплаты в рамках обычного аннуитета могут производиться так часто, как еженедельно, на практике они обычно производятся ежемесячно, ежеквартально, раз в полгода или ежегодно. Противоположностью обычной аннуитета является аннуитет, при котором выплаты производятся в начале каждого периода.Эти две серии платежей не то же самое, что финансовый продукт, известный как аннуитет, хотя они связаны.
Ключевые выводы
- Обычный аннуитет — это серия регулярных платежей, производимых в конце каждого периода, например, ежемесячно или ежеквартально.
- В случае аннуитета, напротив, выплаты производятся в начале каждого периода.
- Стабильные квартальные дивиденды по акциям являются одним из примеров обычной аннуитета; ежемесячная арендная плата является примером подлежащей уплате ренты.
Что такое обычная рента?
Как работает обычная рента
Примерами обычных аннуитетов являются процентные выплаты по облигациям, которые обычно выплачиваются раз в полгода, и квартальные дивиденды по акциям, которые годами поддерживают стабильные уровни выплат. Приведенная стоимость обычного аннуитета во многом зависит от преобладающей процентной ставки.
Из-за временной стоимости денег повышение процентных ставок снижает приведенную стоимость обычного аннуитета, в то время как снижение процентных ставок увеличивает его текущую стоимость.Это связано с тем, что размер аннуитета основан на доходе, который ваши деньги могли бы получить в другом месте. Если вы можете получить более высокую процентную ставку в другом месте, стоимость рассматриваемого аннуитета снизится.
Пример приведенной стоимости обыкновенного аннуитета
Формула приведенной стоимости для обычного аннуитета учитывает три переменные. Вот они:
- PMT = период выплаты наличными
- r = процентная ставка за период
- n = общее количество периодов
С учетом этих переменных приведенная стоимость обычного аннуитета составляет:
- Текущая стоимость = PMT x ((1 — (1 + r) ^ -n) / r)
Например, если обычный аннуитет выплачивает 50 000 долларов в год в течение пяти лет, а процентная ставка составляет 7%, приведенная стоимость будет:
- Текущая стоимость = 50 000 долларов x ((1 — (1 + 0.-5) / 0,07) = 205 010 долл. США
Обычный аннуитет будет иметь более низкую приведенную стоимость, чем аннуитет, при прочих равных.
Приведенная стоимость аннуитета Пример
Напомним, что при обычном аннуитете инвестор получает платеж в конце периода времени. Это контрастирует с аннуитетом, при котором инвестор получает платеж в начале периода. Типичным примером является арендная плата, когда арендатор обычно платит арендодателю заранее за месяц вперед.- (5-1) / 0,07) = 219360 долларов США.
При прочих равных условиях аннуитет всегда стоит больше, чем обычный аннуитет, потому что деньги получены раньше.
Определение таблицы ренты
Что такое аннуитетный стол?
Таблица аннуитета — это инструмент для определения приведенной стоимости аннуитета или другой структурированной серии платежей. Такой инструмент, используемый бухгалтерами, актуариями и другим страховым персоналом, учитывает, сколько денег было внесено в аннуитет и как долго это было, чтобы определить, сколько денег будет причитаться покупателю аннуитета или аннуитету.
Расчет текущей стоимости любой будущей суммы аннуитета также можно выполнить с помощью финансового калькулятора или программного обеспечения, созданного для этой цели.
Ключевые выводы
- Аннуитетная таблица — это инструмент, используемый для определения текущей стоимости аннуитета.
- Таблица аннуитета вычисляет приведенную стоимость аннуитета с использованием формулы, которая применяет ставку дисконтирования к будущим платежам.
- Аннуитетная таблица использует ставку дисконтирования и номер периода для выплаты, чтобы дать вам соответствующий коэффициент.
- Используя аннуитетную таблицу, вы умножите сумму вашего регулярного платежа в долларах на указанный коэффициент.
Как работает аннуитетный стол
Таблица аннуитета предоставляет коэффициент, основанный на времени, и ставку дисконтирования (процентную ставку), на которую можно умножить аннуитетный платеж, чтобы определить его текущую стоимость. Например, аннуитетную таблицу можно использовать для расчета приведенной стоимости аннуитета, по которому выплачивается 10 000 долларов в год в течение 15 лет, если ожидается, что процентная ставка составит 3%.
Согласно концепции временной стоимости денег, получение единовременной выплаты в настоящем имеет большую ценность, чем получение такой же суммы в будущем. Таким образом, иметь 10000 долларов сегодня лучше, чем давать 1000 долларов в год в течение следующих 10 лет, потому что эту сумму можно было бы инвестировать и получать проценты в течение этого десятилетия. В конце 10-летнего периода единовременная выплата в размере 10 000 долларов будет стоить больше, чем сумма ежегодных платежей, даже если они будут инвестированы по той же процентной ставке.
Таблица ренты использует
Победитель лотереи может использовать таблицу аннуитета, чтобы определить, имеет ли финансовый смысл использовать его выигрыш в лотерею в виде единовременной выплаты сегодня или в виде серии платежей в течение многих лет. -n} {r} \\ & \ textbf {where:} \\ & \ text {P} = \ text {Текущая стоимость потока аннуитета} \\ & \ text {PMT} = \ text {Сумма в долларах каждого ежегодного платежа} \\ & r = \ text {Процентная ставка (также известная как ставка дисконтирования) } \\ & n = \ text {Количество периодов, в которые будут производиться выплаты} \ end {выровнено} P = PMT × r1− (1 + r) −n, где: P = текущая стоимость потока аннуитета PMT = сумма в долларах каждого плательщика аннуитета = процентная ставка (также известная как ставка дисконтирования)
Предположим, у человека есть возможность получать аннуитет, который выплачивает 50 000 долларов в год в течение следующих 25 лет со ставкой дисконтирования 6% или единовременную выплату в размере 650 000 долларов.-25} {0,06} = \ 639 168 $ \\ & \ textbf {где:} \\ & \ text {PVA} = \ text {Текущая стоимость ренты} \ end {выровнено} PVA = 50 000 долларов США × 0,061− (1 + 0,06) −25 = 639 168 долларов США, где:
Учитывая эту информацию, аннуитет стоит на 10 832 доллара меньше с поправкой на время, и человек должен выбрать единовременную выплату вместо аннуитета. — n) / r).
Коэффициент определяется процентной ставкой (r в формуле) и количеством периодов, в течение которых будут производиться выплаты (n в формуле). В аннуитетной таблице количество периодов обычно отображается в левом столбце. Процентная ставка обычно указывается в верхней строке. Просто выберите правильную процентную ставку и количество периодов, чтобы найти свой коэффициент в пересекающейся ячейке. Затем этот коэффициент умножается на сумму в долларах аннуитета, чтобы получить приведенную стоимость обычного аннуитета.
Ниже приведен пример приведенной стоимости обычной аннуитетной таблицы:
| n | 1% | 2% | 3% | 4% | 5% | 6% |
| 1 | 0,9901 | 0,9804 | 0,9709 | 0,9615 | 0,9524 | 0,9434 |
| 2 | 1,9704 | 1.9416 | 1,9135 | 1.8861 | 1.8594 | 1.8334 |
| 3 | 2,9410 | 2,8839 | 2,8286 | 2,7751 | 2,7233 | 2,6730 |
| 4 | 3.9020 | 3,8077 | 3,7171 | 3,6299 | 3,5460 | 3,4651 |
| 5 | 4,8534 | 4,7135 | 4.5797 | 4.4518 | 4,3295 | 4,2124 |
| 10 | 9,4713 | 8.9826 | 8,5302 | 8.1109 | 7,7217 | 7.3601 |
| 15 | 13,8651 | 12,8493 | 11.9380 | 11.1184 | 10,3797 | 9,7123 |
| 20 | 18.0456 | 16,3514 | 14,8775 | 13,5903 | 12.4622 | 11,4699 |
| 25 | 22.0232 | 19,5235 | 17.4132 | 15,6221 | 14.0939 | 12,7834 |
Если мы возьмем приведенный выше пример с процентной ставкой 6% и периодом в 25 лет, вы найдете коэффициент = 12,7834. Если вы умножите этот коэффициент 12,7834 из аннуитетной таблицы на сумму платежа в размере 50 000 долларов, вы получите 639 168 долларов. Обратите внимание, это то же самое, что и результат приведенной выше формулы.
Существует отдельная таблица для текущей стоимости подлежащего выплате аннуитета, и она даст вам правильный коэффициент на основе второй формулы.
Аннуитет, подлежащий выплате
Сколько причитается аннуитет?
Аннуитет — это аннуитет, выплата которого производится немедленно в начале каждого периода. Распространенным примером подлежащей выплате аннуитета является арендная плата, поскольку домовладельцы часто требуют выплаты в начале нового месяца, а не взыскания ее после того, как арендатор пользовался льготами от квартиры в течение всего месяца.
Ключевые выводы
- Аннуитет — это аннуитет, выплата которого производится немедленно в начале каждого периода.
- Аннуитет можно сравнить с обычным аннуитетом, когда выплаты производятся в конце каждого периода.
- Типичный пример причитающейся аннуитета — арендная плата, выплачиваемая в начале каждого месяца.
- Пример обычного аннуитета включает ссуды, такие как ипотека.
- Формулы текущей и будущей стоимости подлежащего выплате аннуитета немного отличаются от формул для обычного аннуитета, поскольку они учитывают разницу в сроках осуществления платежей.
Как работает аннуитет
Для выплаты аннуитета требуются выплаты в начале, а не в конце каждого периода аннуитета. Причитающиеся аннуитетные платежи, полученные физическим лицом, по закону представляют собой актив. Между тем, лицо, выплачивающее аннуитет, имеет юридическое долговое обязательство, требующее периодических выплат.
Поскольку серия причитающихся платежей по аннуитету отражает ряд будущих притоков или оттоков денежных средств, плательщик или получатель средств может пожелать рассчитать полную стоимость аннуитета с учетом временной стоимости денег.Этого можно добиться, используя расчеты приведенной стоимости.
В таблице приведенной стоимости подлежащего выплате аннуитета прогнозируемая процентная ставка указана в верхней части таблицы, а количество периодов — в крайнем левом столбце. Пересекающаяся ячейка между соответствующей процентной ставкой и количеством периодов представляет множитель приведенной стоимости. Нахождение продукта между одним причитающимся платежом по аннуитету и множителем приведенной стоимости дает текущую стоимость денежного потока.
Причитающийся пожизненный аннуитет — это финансовый продукт, продаваемый страховыми компаниями, который требует выплаты аннуитета в начале каждого ежемесячного, ежеквартального или годового периода, а не в конце периода.Это тип аннуитета, который будет обеспечивать держателя выплат в течение периода распределения на протяжении всей его жизни. После того, как аннуитет переходит, страховая компания удерживает оставшиеся средства.
Доходные выплаты по аннуитету облагаются налогом как обычный доход.
Причитающаяся рента против обычной ренты
Причитающаяся аннуитетная выплата — это повторяющаяся выдача денег в начале периода. В качестве альтернативы, обычная аннуитетная выплата представляет собой повторяющуюся выдачу денег в конце периода.Контракты и деловые соглашения определяют этот платеж, и он зависит от того, когда была получена выгода. При оплате расходов получатель уплачивает причитающуюся аннуитетную выплату до получения пособия, в то время как получатель производит обычные платежи после выплаты пособия.
Время выплаты аннуитета имеет решающее значение с учетом альтернативных издержек. Сборщик платежа может инвестировать аннуитетный платеж, полученный в начале месяца, для получения процентов или прироста капитала.Вот почему аннуитет более выгоден для получателя, поскольку у него есть возможность быстрее использовать средства. В качестве альтернативы, люди, выплачивающие аннуитет, теряют возможность использовать средства в течение всего периода. Таким образом, выплачивающие аннуитеты, как правило, предпочитают обычные аннуитеты.
Примеры аннуитета
Аннуитет может возникнуть в связи с любыми повторяющимися обязательствами. Многие ежемесячные счета, такие как аренда, ипотека, оплата автомобиля и сотового телефона, являются аннуитетами, поскольку получатель должен оплатить в начале расчетного периода.Расходы на страхование обычно представляют собой аннуитетные выплаты, поскольку страховщик требует выплаты в начале каждого периода страхового покрытия. Ситуации, связанные с выплатой аннуитета, также обычно возникают в связи с накоплением на пенсию или откладыванием денег на определенную цель.
Как рассчитать размер аннуитета
Настоящая и будущая стоимость причитающейся аннуитета может быть рассчитана с использованием небольших изменений текущей стоимости и будущей стоимости обычной аннуитета.
Приведенная стоимость аннуитета к уплате
Приведенная стоимость причитающейся аннуитета показывает нам текущую стоимость ряда ожидаемых аннуитетных платежей.Другими словами, он показывает, сколько сейчас стоит будущая сумма, подлежащая выплате.
Расчет приведенной стоимости подлежащей выплате аннуитета аналогичен расчету текущей стоимости обычного аннуитета. Однако есть тонкие различия, которые необходимо учитывать при наступлении срока выплаты аннуитета. Для причитающегося аннуитета выплаты производятся в начале интервала, а для обычного аннуитета выплаты производятся в конце периода. Формула для определения текущей стоимости причитающегося аннуитета:
Приведенная стоимость причитающейся аннуитета.ИнвестопедияС:
- C = Денежные потоки за период
- i = процентная ставка
- n = количество платежей
Давайте посмотрим на пример приведенной стоимости подлежащего выплате аннуитета. Предположим, вы являетесь бенефициаром, которому назначено немедленное получение 1000 долларов в год в течение 10 лет с годовой процентной ставкой 3%. Вы хотите знать, сколько стоит для вас поток платежей сегодня. Согласно формуле приведенной стоимости, приведенная стоимость составляет 8 786 долларов.11.
Приведенная стоимость аннуитета. ИнвестопедияБудущая стоимость аннуитета к уплате
Будущая стоимость подлежащего выплате аннуитета показывает нам конечную стоимость ряда ожидаемых платежей или стоимость в будущем.
Подобно тому, как существуют различия в том, как рассчитывается приведенная стоимость для обычного аннуитета и аннуитета к выплате, существуют также различия в том, как рассчитывается будущая стоимость денег для обычного аннуитета и подлежащего выплате аннуитета. Будущая стоимость аннуитета рассчитывается как:
Будущая стоимость аннуитета.ИнвестопедияИспользуя тот же пример, мы вычисляем, что будущая стоимость потока выплат дохода будет 11 807,80 долларов США.
Будущая стоимость аннуитета. ИнвестопедияЧасто задаваемые вопросы о выплате аннуитета
Что лучше: обычная рента или рента с уплатой?
Что лучше — обычная аннуитет или аннуитет, зависит от того, являетесь ли вы получателем или плательщиком. Как получатель платежа, аннуитет часто предпочтительнее, потому что вы получаете аванс на определенный срок, что позволяет вам использовать средства немедленно и получать более высокую приведенную стоимость, чем у обычного аннуитета.Для плательщика обычная рента может быть выгодной, поскольку вы вносите платеж в конце срока, а не в начале. Вы можете использовать эти средства в течение всего периода до оплаты.
Часто вам не предоставляется возможность выбора. Например, страховые взносы являются примером подлежащего уплате аннуитета, при этом взносы должны быть уплачены в начале страхового периода. Плата за автомобиль является примером обычного аннуитета, при котором платежи подлежат оплате в конце периода покрытия.
Что такое немедленная рента?
Немедленный аннуитет — это счет, финансируемый за счет единовременного депозита, который генерирует немедленный поток выплат дохода.Доход может составлять заявленную сумму (например, 1000 долларов в месяц), заявленный период (например, 10 лет) или всю жизнь.
Как рассчитать будущую стоимость причитающейся ренты?
Будущая стоимость аннуитета рассчитывается по формуле:
Будущая стоимость аннуитета. Инвестопедиякуда
- C = Денежные потоки за период
- i = процентная ставка
- n = количество платежей
Что означает аннуитет?
Аннуитет — это страховой продукт, предназначенный для генерирования платежей сразу или в будущем владельцу аннуитета или назначенному получателю.Владелец счета производит либо единовременный платеж, либо серию платежей в аннуитет и может либо получать немедленный поток дохода, либо отложить получение платежей до некоторого времени в будущем, обычно после периода накопления, когда на счете начисляются отсроченные по налогу на прибыль проценты. .
Что происходит по истечении срока годности?
По истечении срока годности договор прекращается, и будущие платежи не производятся. Обязательства по контракту выполнены, и ни одна из сторон не возьмет на себя никаких дальнейших обязательств.
Итог
Причитающийся аннуитет — это аннуитет с выплатой, подлежащей выплате или произведенной в начале платежного интервала. Напротив, при обычном аннуитете выплаты производятся в конце периода. В результате методы расчета текущей и будущей стоимости различаются. Типичный пример причитающейся аннуитета — арендная плата, выплачиваемая домовладельцу, а типичный пример обычного аннуитета включает выплаты по ипотеке, произведенные кредитору. В зависимости от того, плательщик вы или получатель, аннуитет может быть лучшим вариантом.
Приведенная стоимость аннуитета Определение
Какова приведенная стоимость аннуитета?
Приведенная стоимость аннуитета — это текущая стоимость будущих выплат из аннуитета при заданной норме доходности или ставке дисконтирования. Чем выше ставка дисконтирования, тем ниже приведенная стоимость аннуитета.
Ключевые выводы
- Приведенная стоимость аннуитета относится к тому, сколько денег потребовалось бы сегодня для финансирования серии будущих аннуитетных платежей.
- Из-за временной стоимости денег сумма денег, полученная сегодня, стоит больше, чем такая же сумма в будущем.
- Вы можете использовать расчет приведенной стоимости, чтобы определить, получите ли вы больше денег, взяв единовременную выплату сейчас или выплачивая аннуитет на несколько лет.
Понимание приведенной стоимости аннуитета
Из-за временной стоимости денег деньги, полученные сегодня, стоят больше, чем такая же сумма денег в будущем, потому что их можно инвестировать тем временем.По той же логике, 5000 долларов, полученные сегодня, стоят больше, чем та же сумма, распределенная на пять ежегодных взносов по 1000 долларов каждый.
Будущая стоимость денег рассчитывается с использованием ставки дисконтирования. Под ставкой дисконтирования понимается процентная ставка или предполагаемая норма прибыли по другим инвестициям в течение того же срока, что и выплаты. Наименьшая ставка дисконтирования, используемая в этих расчетах, — это безрисковая норма прибыли. n} \ Big)} {r} \\ & \ textbf {где:} \\ & \ text {P} = \ text {Текущая стоимость потока аннуитета} \\ & \ text {PMT} = \ text {Сумма в долларах каждого ежегодного платежа} \\ & r = \ text {Процентная ставка (также известная как ставка дисконтирования)} \\ & n = \ text {Количество периодов, в течение которых будут производиться платежи} \\ \ end {выровнено} P = PMT × r1 — ((1 + r) n1) где: P = текущая стоимость потока аннуитета PMT = сумма в долларах каждого плательщика аннуитета = процентная ставка (также известная как ставка дисконтирования) n = количество периодов в какие выплаты будут производиться
Предположим, у человека есть возможность получить обычную ренту, которая выплачивает 50 000 долларов в год в течение следующих 25 лет со ставкой дисконтирования 6%, или получить единовременную выплату в размере 650 000 долларов.{25}} \ Big)} {0,06} \\ & = \ $ 639 168 \\ \ end {выровнено} Текущая стоимость = 50 000 долларов США × 0,061 — ((1 + 0,06) 251) = 639 168 долларов США.
Учитывая эту информацию, аннуитет будет стоить на 10 832 доллара меньше с поправкой на время, так что человек выйдет вперед, выбрав единовременную выплату над аннуитетом.
При обычном аннуитете выплаты производятся в конце каждого периода времени, а при уплате аннуитета — в начале. При прочих равных условиях годовая рента будет стоить больше в настоящее время.{25}} \ Big)} {0,06} \ times (1 + 0,06) \\ & = \ 677 518 долларов \\ \ end {выровнено} Текущая стоимость = 50 000 долларов США × 0,061 — ((1 + 0,06) 251) × (1 + 0,06) = 677 518 долларов США.
В этом случае человек должен выбрать вариант выплаты аннуитета, потому что он стоит на 27 518 долларов больше, чем единовременная выплата на 650 000 долларов.
Часто задаваемые вопросы
Почему будущая стоимость (FV) важна для инвесторов?
Будущая стоимость (FV) — это стоимость текущего актива на дату в будущем, основанную на предполагаемой скорости роста.Это важно для инвесторов, поскольку они могут использовать его, чтобы оценить, сколько инвестиций, сделанных сегодня, будет стоить в будущем. Это поможет им в принятии обоснованных инвестиционных решений с учетом их предполагаемых потребностей. Однако внешние экономические факторы, такие как инфляция, могут отрицательно повлиять на будущую стоимость актива, снижая его стоимость.
Чем обычная рента отличается от подлежащей уплате ренты?
Обычный аннуитет — это серия равных платежей, производимых в конце последовательных периодов в течение фиксированного периода времени.Пример обычного аннуитета включает ссуды, такие как ипотека. Оплата аннуитета производится в начале каждого периода. Типичный пример причитающейся аннуитета — арендная плата. Эта разница в сроках осуществления платежей приводит к различным расчетам настоящей и будущей стоимости.
Какова формула приведенной стоимости обычной ренты?
Формула приведенной стоимости обычного аннуитета:
п знак равно ГУП × 1 — ( 1 ( 1 + р ) п ) р куда: п знак равно Приведенная стоимость потока аннуитета ГУП знак равно Сумма в долларах каждого аннуитетного платежа р знак равно Процентная ставка (также известная как ставка дисконтирования) п знак равно Количество периодов, в которые будут производиться выплаты \ begin {align} & \ text {P} = \ text {PMT} \ times \ frac {1 — \ Big (\ frac {1} {(1 + r) ^ n} \ Big)} {r} \\ & \ textbf {где:} \\ & \ text {P} = \ text {Текущая стоимость потока аннуитета} \\ & \ text {PMT} = \ text {Сумма в долларах каждого ежегодного платежа} \\ & r = \ text {Процентная ставка (также известная как ставка дисконтирования)} \\ & n = \ text {Количество периодов, в течение которых будут производиться платежи} \\ \ end {выровнено} P = PMT × r1 — ((1 + r) n1) где: P = текущая стоимость потока аннуитета PMT = сумма в долларах каждого плательщика аннуитета = процентная ставка (также известная как ставка дисконтирования) n = количество периодов в какие выплаты будут производиться
Какова формула для определения приведенной стоимости аннуитета?
Формула выплаты аннуитета, при котором выплаты производятся в начале каждого периода, немного отличается от формулы обычного аннуитета.


 {-N} \over r \right] (1+r) } \)
{-N} \over r \right] (1+r) } \) {19}} \over 0.07 \right] \end{aligned} } \)
{19}} \over 0.07 \right] \end{aligned} } \) {30}} \over 0.05 \right] \end{aligned} } \)
{30}} \over 0.05 \right] \end{aligned} } \) t \right] } \) (формула 12)
t \right] } \) (формула 12)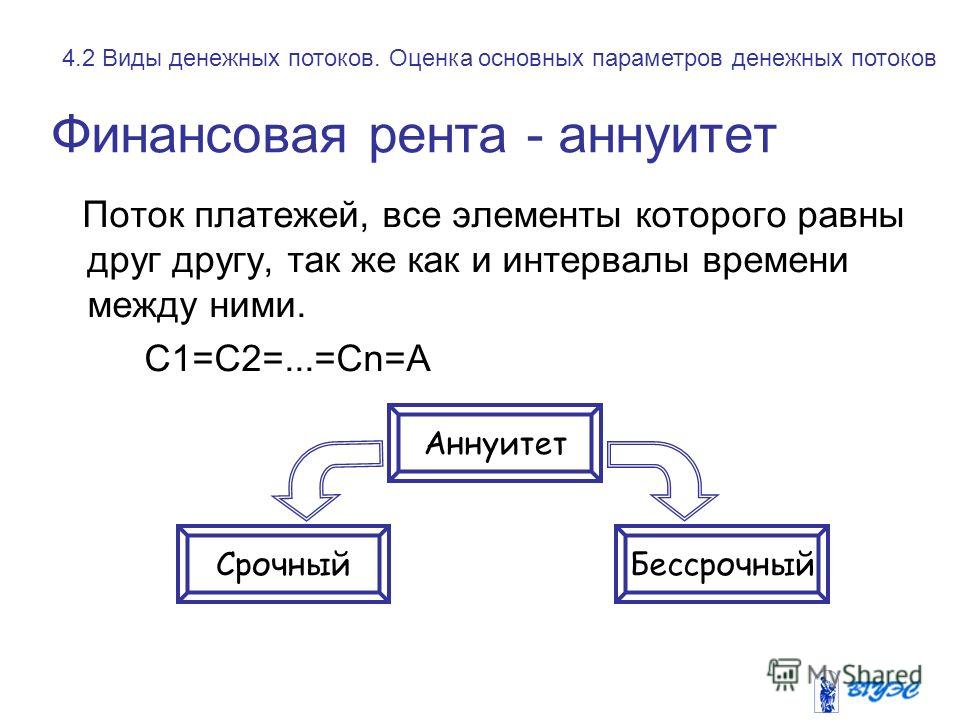 В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.
В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0. 05
05

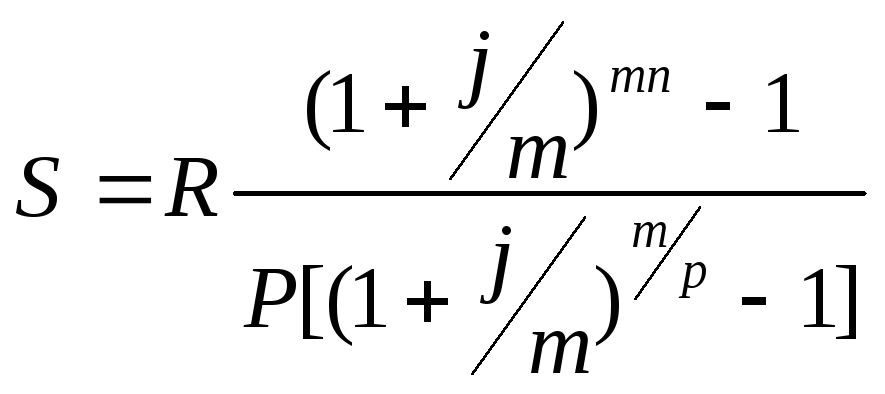

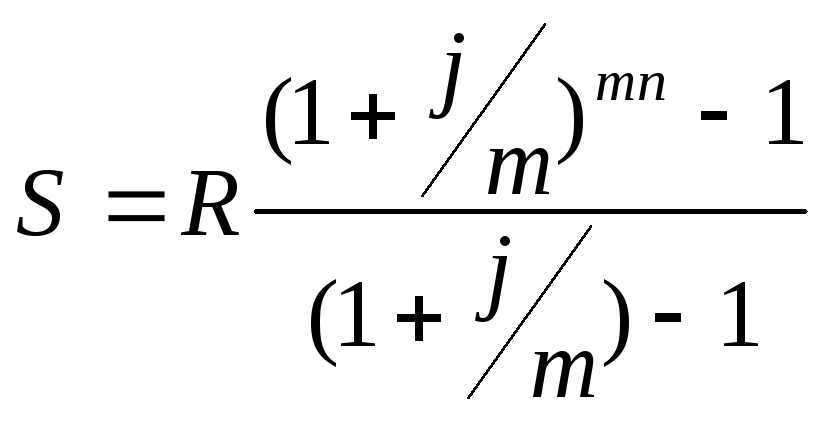
 38
38 46
46 начало:
начало: ‘perpetuity’ или ‘perpetual annuity’) — это бесконечная (бессрочная) серия потоков денежных средств. При этом первый денежный поток происходит через один период (т.е. t = 1).
‘perpetuity’ или ‘perpetual annuity’) — это бесконечная (бессрочная) серия потоков денежных средств. При этом первый денежный поток происходит через один период (т.е. t = 1).
 N — 1} \over r \right] }$$
N — 1} \over r \right] }$$
 77 к моменту выхода на пенсию.
77 к моменту выхода на пенсию.
 05)1 =
05)1 =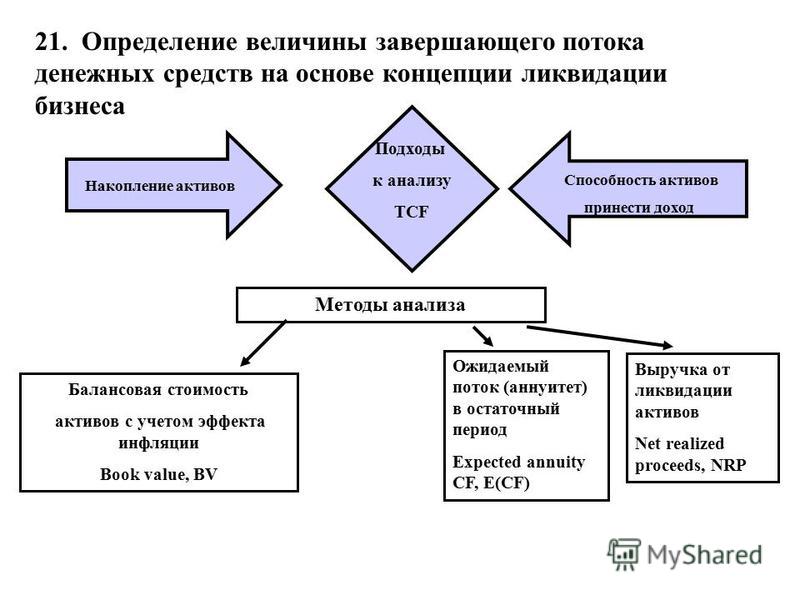
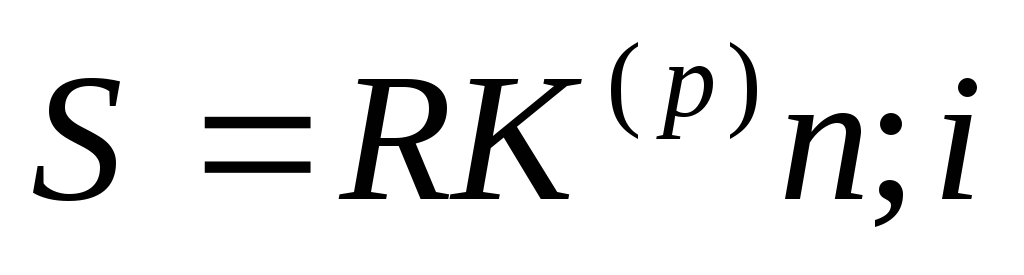
 н. обратная задача предполагает суммарную оценку дисконтированного (приведенного) денежного потока.
н. обратная задача предполагает суммарную оценку дисконтированного (приведенного) денежного потока.
 В этом случае аннуитет называется переменным.
В этом случае аннуитет называется переменным.